Комплексные числа. Операции над ними...

Глава 4: Комплексные числа:

Комплексным числом называется выражение вида a + bi, где a и b — вещественные числа, i — элемент, так называемая, мнимая единица, не принадлежащий R(множеству действительных чисел).

Рассмотрим комплексное число z = a + bi. Число a называется действительной частью комплексного числа, b — мнимой частью, и обозначаются Re(z) и Im(z), соответственно.

Пример: Для комплексного числа z = 3 − 2i имеем, Re(z) = 3, Im(z) = −2.

Замечание: Любое вещественное число a можно рассматривать как комплексное число a + 0i. Таким образом, множество вещественных чисел лежит в множестве комплексных чисел.

Два комплексных числа будем считать равными тогда и только тогда, когда совпадают их вещественные и мнимые части. Множество комплексных чисел обозначается буквой C.

4.1: Арифметические операции:

На множестве комплексных чисел введем две операции: сложение и умножение. Пусть даны два комплексных числа z = a + bi, w = c + di. Тогда

• z + w = (a + c) + (b + d)i;
• zw = (ac − bd) + (ad + bc)i.

Введенные операции обладают всеми хорошими свойствами, такими же как операции сложения и умножения на множестве вещественных чисел (ассоциативностью, коммутативностью, дистрибутивностью).

Пример 20. Для мнимой единицы i можно легко составить таблицу jумножения: i² = −1, i³ = −i, i⁴ = 1 и т.д. 

Упражнение: вычислите, чему равно выражение i⁵⁹

Подчеркнем еще раз важное свойство мнимой единицы: i² = −1.

По аналогии с операциями на R на множестве комплексных чисел можно ввести операции вычитания и деления. Для комплексных чисел z = a + bi и w = c + di определим

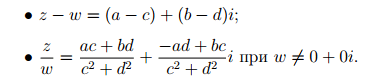
Пусть дано комплексное число z = a + bi. Комплексно сопряженным к числу z называется число a − bi и обозначается через z. Рассмотрим некоторые свойства комплексного сопряжения. Для любых комплексных числ z, z1, z2 выполнено

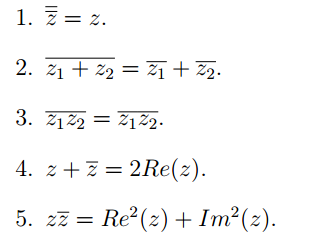
Простое правило для выполнения деления комплексных чисел. Для того, чтобы вычислить выражение w zс комплексными числами z и w, нужно и числитель, и знаменатель умножить на комплексно сопряженное к знаменателю.

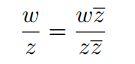
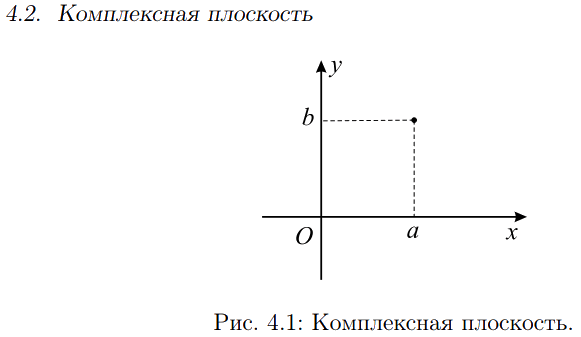
4.2: Комплексная плоскость 

Геометрической интерпретацией комплексных чисел является так называемая комплексная плоскость. На плоскости введем декартову (прямоугольную) систему координат. Каждой точке плоскости с координатами (a, b) сопоставим комплексное число a + bi. Такое сопоставление является взаимно однозначным. Ось абсцисс называется действительной осью, ось ординат — мнимой осью. 
На плоскости можно ввести полярную систему координат, ассоциированную декартовой. Тогда любая точка плоскости задается парой чисел: длиной радиус-вектора и углом поворота.

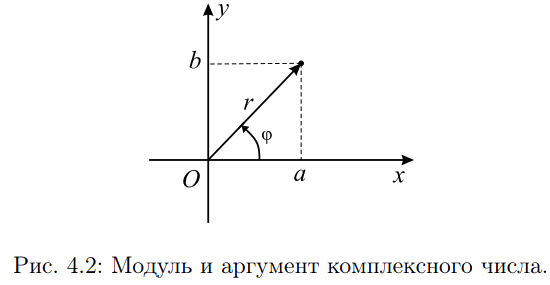
Длина радиус вектора, отвечающего комплексному числу z = a + bi, называется модулем этого числа и обозначается |z| или r. Справедлива формула 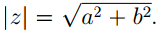. Величина угла между положительным направлением действительной оси и радиус вектором, отвечающим комплексному числу, называется аргументом этого числа и обозначается arg z или φ. Следующие формулы имеют место 

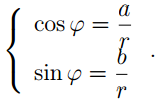
4.3: Тригонометрическая форма

Форма записи комплексного числа a+bi называется алгебраической. Это форма удобна для сложения и вычитания комплексных чисел. Перейдя в полярную систему координат на комплексной плоскости (a = r cos φ и b = r sin φ), любое комплексное число z = a + bi можно представить в виде:

z = r(cos φ + isin φ).

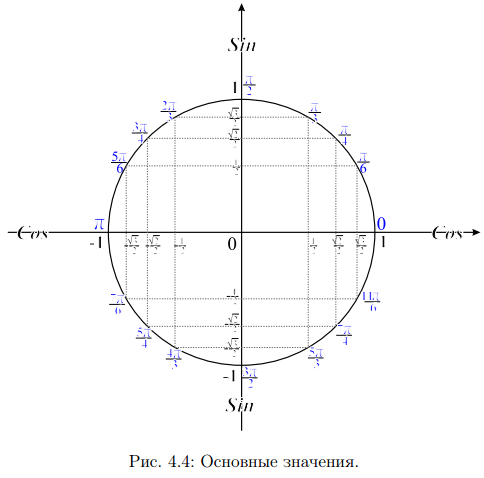
Такая запись называется тригонометрической формой комплексного числа z. Здесь число r —  модуль комплексного числа z, φ — аргумент числа z. На рис. 4.4 изображена единичная окружность с основными табличными значениями синуса и косинуса.