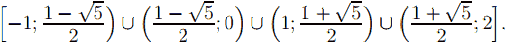Решите неравенство: 1 / (log ^(x^2 - x) 0,5) + 1 / (log^(x...

Задание:

Решите неравенство: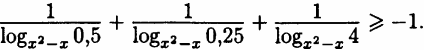 

Решение:

ОДЗ неравенства является множество всех решений системы

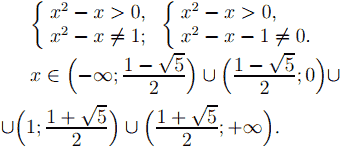
Перейдём в неравенстве к логарифмам по основанию 2.

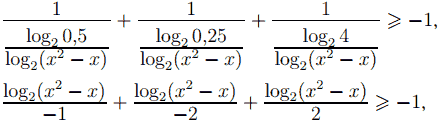
log₂ (x² − x) * (−1 − 1/2 + 1/2) ≥ −1, − log₂ (x² − x) ≥ −1, log₂ (x² − x) ≤ 1.

log₂ (x² − x) ≤ log₂ 2, x² − x ≤ 2, x² − x − 2 ≤ 0.

Находим корни квадратного трёхчлена x² − x − 2: x_1,2 = (1 ± √9) / 2 , x₁ = −1, x₂ = 2, поэтому множеством решений неравенства будет множество [−1; 2].

Так как −1 < 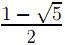 < 0 и 1 <  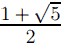< 2, то множеством решений неравенства будет множество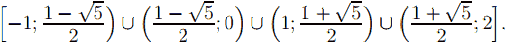 

Ответ: