Решите неравенство log^|x - 5|(2х^2 - 10х + 8) ≤ 2.

Задание:

Решите неравенство log_{|x - 5|}(2х² - 10х + 8) ≤ 2.

Решение:

log_|x−5|(2x² − 10x + 8) ≤ 2.

ОДЗ:

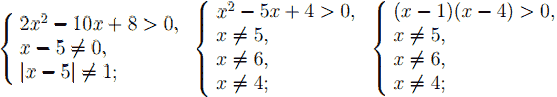
x ∈ (−∞; −1) ∪ (4; 5) ∪ (5; 6) ∪ (6; ∞).

log_|x−5|(2x² − 10x + 8) ≥ log_|x−5|(x − 5)²,

log_|x−5|(2x² − 10x + 8) − log_|x−5|(x − 5)² ≤ 0.

На ОДЗ заменим неравенство равносильными неравенствами, применив дважды метод рационализации:

1) знак loga f − log_a g совпадает со знаком (a − 1)(f − g),

2) знак |f| − |g| совпадает со знаком (f − g)(f + g).

Применяем 1: (|x − 5| − 1)(2x² − 10x + 8 − x² + 10x − 25) ≤ 0,

(|x − 5| − 1)(x² − 17) ≤ 0.

Применяем 2: (x − 5 − 1)(x − 5 + 1)(x² − 17) ≤ 0.

(x − 6)(x − 4)(x − √17)(x + √17) ≤ 0.

− √17 ≤ x ≤ 4, √17 ≤ x ≤ 6.

Учитывая ОДЗ, получим: − √17 ≤ x < 1; √17 ≤ x < 5; 5 < x < 6.

Ответ: [− √17; 1) ∪ [√17; 5) ∪ (5; 6).