Точка Р — центр окружности, описанной около остроуг...

Задание:

Точка Р — центр окружности, описанной около остроугольного треугольника MNQ , К — центр вписанной в него окружности, О — точка пересечения высот. Известно, что ∠NMQ = ∠PNQ  + ∠PQN.

а) Докажите, что точка К лежит на окружности, описанной около треугольника NPQ.

б) Найдите угол РКО, если ∠MNQ = 42°.

Решение:

а) Чтобы доказать, что точки N, P, K и Q лежат на одной окружности, можно воспользоваться одним из признаков, например доказать, что ∠NPQ = ∠NKQ. Найдём эти углы.

P — центр окружности, описанной около треугольника MNQ, тогда как центральный и вписанный углы, опирающиеся на одну дугу, ∠NPQ = 2∠NMQ.

Запишем сумму углов треугольника NPQ и воспользуемся полученным и заданным в условии равенствами.

∠NPQ + ∠PNQ + ∠PQN = 2∠NMQ + ∠NMQ = 3∠NMQ = 180◦ ,

∠NMQ = 180◦ : 3 = 60◦ ; ∠NPQ = 2 · 60◦ = 120◦ .

K — центр вписанной в треугольник MNQ окружности, поэтому K — точка пересечения биссектрис треугольника.

∠NKQ = 180◦ − (∠KNQ + ∠KQN) = 180◦ − (∠MNQ + ∠MQN) / 2 .

∠NKQ = 180◦ − (180◦ − ∠NMQ) / 2 = 120◦ .

Значит, ∠NPQ = ∠NKQ, поэтому точки N, P, K и Q лежат на одной окружности.

б) O — точка пересечения высот треугольника NMQ. Найдём угол PKO, для этого докажем сначала, что и точка O лежит на той же окружности, что и точки N, P, K и Q.

Если провести высоту треугольника (например, из вершины N), то образуются прямоугольные треугольники, сумма острых углов каждого такого треугольника равна 90◦ . Например, ∠ONQ + ∠MQN = 90◦ , аналогично можно получить: ∠OQN + ∠MNQ = 90◦ . ∠NOQ = 180◦ − ∠ONQ − ∠OQN = 180◦ − (90◦ − ∠MQN) − (90◦ − ∠MNQ) = ∠MQN + ∠MNQ = 180◦ − ∠NMQ = 120◦ .

Значит, ∠NPQ = ∠NKQ = ∠NOQ, потому точки N, P, K, O и Q лежат на одной окружности.

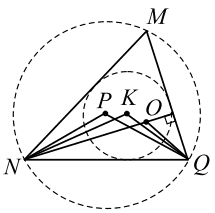
∠NMQ = 60◦ , ∠MNQ = 42◦ , получаем: ∠MQN = 180◦ − 60◦ − 42◦ = 78◦ . В равнобедренном треугольнике NPQ имеем ∠PNQ = (180◦ − ∠NPQ) / 2 = 30◦ . Учитывая, что NO ⊥ MQ, получаем: ∠ONQ = 90◦ − ∠MQN = 12◦ .

Отсюда ∠ONP = ∠PNQ − ∠ONQ = 30◦ − 12◦ = 18◦ . Имеем: ∠PNQ = 30◦ , ∠KNQ = ∠MNQ / 2 = 42◦ / 2 = 21◦ , ∠ONQ = 90◦ − ∠MQN = 90◦ − 78◦ = 12◦ , значит, ∠PNQ > ∠KNQ > ONQ, поэтому лучи NO, NK и NP пересекают дугу окружности в порядке, указанном на рисунке. Четырёхугольник NPKO вписан в окружность, поэтому ∠PKO = 180◦ − ∠ONP = 180◦ − 18◦ = 162◦ .

Ответ: б) 162◦.