Алгоритм Дейкстры. Алгоритм Форда-Беллмана

Алгоритм Дейкстры. Алгоритм Форда-Беллмана. Язык: С

Сегодня разберем два алгоритма для поиска минимального пути от любой вершины графа до любой другой вершины.

Первый алгоритм - Дейкстры.  

Алгоритм работает только для графов без ребер отрицательного веса.

Второй алгоритм - Форда-Беллмана. 

В отличие от предыдущего алгоритма, этот работает при наличии в графах ребер отрицательного веса.  Алгоритм также позволяет узнать есть ли в графе отрицательный цикл. Если вместо  |V| - 1  итераций сделать |V| итераций цикла и длина кратчайшей пути до какой-либо вершины уменьшилась, то граф содержит отрицательный цикл.

|V| - число ребер в графе.

На входе программы: файл, в первой строке которой - порядок матрицы, далее идет матрица смежности взвешенного графа.

На выходе:  массив с расстояниями от заданной вершины до всех остальных,  если пути нет, то выводим "INF".

Также программа считает время выполнения алгоритмов и выводит на экран.

Программа реализована в visual studio 2017 

Скачать примеры тест-файлов

Реализация на языке Си: 

#include "stdio.h"
#include "malloc.h"
#include "locale.h"
#include "time.h"
#define INF 1000000000

void output(int count, int* result, int apex, int mode)
{
    int i;
    if (mode == 0)
        printf("Дейкстра:\n");
    else
        printf("Форд-Баллман:\n");

    for (i = 0; i < count; i++)
    {
        //если путь есть
        if (result[i] < 10000)
            printf("Минимальное расстояние между вершинами %d и %d = %d\n", apex,\
 i, result[i]);
        else
            printf("Минимальное расстояние между вершинами %d и %d = INF\n", apex,\
 i);
    }
}


void Ford_Ballman(int CountApex, int** SourceMatrix, int Start)
{
    int *MinPath; // массив кратчайших путей
    int i, j, k;
    int count = 0;
    MinPath = (int*)malloc(CountApex * sizeof(int));

    for (i = 0; i<CountApex; i++)
    {
        MinPath[i] = INF; //изначально кратчайшие пути неизвестны
    }

    MinPath[Start] = 0;
    for (k = 0; k<CountApex; k++)
    {
        for (i = 0; i < CountApex; ++i)
        {
            for (j = 0; j < CountApex; ++j)
            {
                if (SourceMatrix[i][j] != 0) //если вершину не посещали
                    if (MinPath[j] > MinPath[i] + SourceMatrix[i][j])
                        MinPath[j] = MinPath[i] + SourceMatrix[i][j];
            }
        }
    }
    output(CountApex, MinPath, Start, 1);
}

void deikstra(int CountApex, int** SourceMatrix, int Start)
{
    int *metka; // массив меток
    int *MinPuth; // массив кратчайших путей
    int temp, i;
    int minindex, min;
    metka = (int*)malloc(CountApex * sizeof(int));
    MinPuth = (int*)malloc(CountApex * sizeof(int));
    for (i = 0; i<CountApex; i++) {
        MinPuth[i] = INF;
        metka[i] = 1;
    }

    MinPuth[Start] = 0;
    do { // исполнение алгоритма 
        minindex = INF;
        min = INF;
        for (i = 0; i<CountApex; i++) {
            if ((metka[i] == 1) && (MinPuth[i]<min)) {
                min = MinPuth[i];
                minindex = i;
            }
        }

        if (minindex != INF) {
            for (i = 0; i<CountApex; i++) {
                if (SourceMatrix[minindex][i] > 0) {
                    temp = min + SourceMatrix[minindex][i];
                    if (temp < MinPuth[i])
                        MinPuth[i] = temp;
                }
            }
            metka[minindex] = 0;
        }

    } while (minindex < INF);
    output(CountApex, MinPuth, Start, 0);
}

int main(int argc, char* argv)
{
    int apex;
    int CountApex;
    int **mputh;
    int i, j, E = 0;
    int negative = 0;
    float start, end;
    setlocale(LC_ALL, "Rus");
    FILE *in;
    char filename[20];

    printf("Введите имя файла: ");
    scanf_s("%s", filename, 20);
    fopen_s(&in, filename, "r");

    if (!in)
        printf("Ошиба! Файл не прочитан");
    else
        printf("Читаем граф!\n");

    fscanf_s(in, "%d", &CountApex);

    mputh = (int **)malloc(CountApex * sizeof(int *));
    for (int i = 0; i < CountApex; i++) {
        mputh[i] = (int *)malloc(CountApex * sizeof(int));
    }

    for (i = 0; i < CountApex; i++)
    {
        for (j = 0; j < CountApex; j++)
        {
            fscanf_s(in, "%d", &mputh[i][j]);
            if (mputh[i][j] < 0)
                negative++;
        }
    }

    printf("Граф считан\n");
    printf("Введите вершину, от которой ведем отсчет: ");
    scanf_s("%d", &apex);
    start = clock();
    deikstra(CountApex, mputh, apex);
    end = clock();
    printf("Алгоритм использовал %.10f секунд.\n", (end - start) / (CLOCKS_PER_SEC));

    if (negative != 0)
        printf("Матрица содержит ребра с отрицательным весом,\
 алгоритм Дейкстры может работать некорректно\n");

    printf("\n\n");
    start = clock();
    Ford_Ballman(CountApex, mputh, apex);
    end = clock();
    printf("Алгоритм использовал %.10f секунд.\n", (end - start) / (CLOCKS_PER_SEC));
    getchar();
    getchar();
    return 0;
}

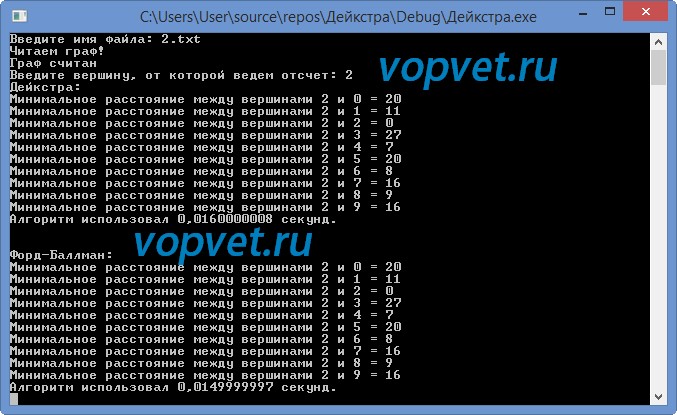
Пример работы программы: