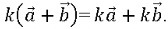Анализ геометрических высказываний. ОГЭ по математике
Категория: Разное
Огромный сборник геометрических утверждений, которые могут попасться на ОГЭ.
| Утверждение | Верно? |
| Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, делит основание на две равные части. | Да |
| Внешний угол треугольника больше каждого не смежного с ним внутреннего угла. | Да |
| В прямоугольном треугольнике катет больше гипотенузы. | Нет |
| В треугольнике АВС, для которого АВ = 4, ВС = 5, АС = 6, угол B — наибольший. | Да |
| Диагонали параллелограмма пересекаются под прямым углом и в точке пересечения делятся пополам. | Нет |
| Биссектриса равнобедренного треугольника, проведённая из вершины перпендикулярна основанию. | Да |
| Биссектриса треугольника делит пополам сторону, к которой проведена? | Нет |
| Биссектриса угла делит угол пополам. | Да |
| Биссектриса угла любого параллелограмма является его диагональю. | Нет |
| Биссектриса угла треугольника делит противоположную сторону на отрезки, пропорциональные двум другим сторонам. | Да |
| Биссектрисы смежных углов взаимно перпендикулярны. | Да |
| Биссектрисы треугольника не могут пересекаться в одной точке | Нет |
| Биссектрисы треугольника пересекаются в одной точке, которая является центром окружности, описанной около этого треугольника. | Нет |
| Биссектрисы треугольника пересекаются в центре его вписанной окружности. | Да |
| Биссектрисы углов параллелограмма прилежащих к одной стороне, пересекаются под прямым углом. | Да |
| Вертикальные углы равны. | Да |
| В каждом треугольнике углы при основании равны. | Нет |
| В квадрате диагонали пересекаются под прямым углом. | Да |
| В любой выпуклый семиугольник можно вписать окружность. | Нет |
| В любой прямоугольник можно вписать окружность. | Нет |
| В любой прямоугольный треугольник можно вписать окружность. | Да |
| В любой ромб можно вписать окружность. | Да |
| В любой трапеции диагонали перпендикулярны. | Нет |
| В любой трапеции диагонали равны. | Нет |
| В любой треугольник можно вписать окружность. | Да |
| В любой четырёхугольник можно вписать не более одной окружности. | Да |
| В любой четырёхугольник можно вписать окружность. | Нет |
| В любом выпуклом четырёхугольнике все углы острые. | Нет |
| В любом выпуклом четырёхугольнике все углы прямые. | Нет |
| В любом выпуклом четырёхугольнике все углы тупые. | Нет |
| В любом описанном около окружности четырехугольнике суммы противоположных сторон равны. | Да |
| В любом описанном четырёхугольнике сумма противоположных углов равна 180°. | Да |
| В любом параллелограмме диагонали равны. | Нет |
| В любом параллелограмме диагонали точкой пересечения делятся пополам. | Да |
| В любом прямоугольнике все стороны равны. | Нет |
| В любом прямоугольнике диагонали взаимно перпендикулярны. | Нет |
| В любом прямоугольнике диагонали равны. | Да |
| В любом равнобедренном треугольнике медиана, проведённая из вершины основания, является биссектрисой и высотой. | Да |
| В любом ромбе диагонали перпендикулярны. | Да |
| В любом треугольнике выполняется теорема Пифагора. | Нет |
| В любом треугольнике против большего угла лежит большая сторона. | Да |
| В любом треугольнике против большей стороны лежит меньший угол. | Нет |
| В любом треугольнике сумма двух сторон больше третьей стороны. | Да |
| В любом треугольнике сумма двух сторон меньше третьей стороны. | Нет |
| В любом тупоугольном треугольнике есть острый угол. | Да |
| В любую окружность можно вписать два подобных, но неравных треугольника. | Нет |
| В любую окружность можно вписать прямоугольник. | Да |
| В любую равнобедренную трапецию можно вписать окружность. | Нет |
| Внешний угол треугольника больше каждого внутреннего угла. | Нет |
| Внешний угол треугольника больше не смежного с ним внутреннего угла. | Да |
| Внешний угол треугольника всегда тупой. | Нет |
| Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним. | Да |
| Внешний угол треугольника равен сумме его внутренних углов. | Нет |
| Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны. | Да |
| Во всякий четырёхугольник можно вписать окружность. | Нет |
| Во всяком треугольнике биссектриса угла равна его медиане. | Нет |
| Во всяком треугольнике высота проведённая к основанию, совпадает с медианой. | Нет |
| Вокруг любого выпуклого восьмиугольника можно описать окружность. | Нет |
| Вокруг любого параллелограмма можно описать окружность. | Нет |
| Вокруг любого треугольника можно описать окружность. | Да |
| Вокруг любого четырёхугольника можно описать окружность. | Нет |
| Вокруг параллелограмма всегда можно описать окружность. | Нет |
| Вокруг равнобедренной трапеции можно описать окружность. | Да |
| Вокруг тупоугольного треугольника нельзя описать окружность. | Нет |
| В окружности на диаметр опирается прямой угол. | Да |
| В окружности радиуса 2 можно провести хорду длиной 3. | Да |
| В окружность можно вписать угол, равный 200° | Нет |
| В параллелограмме все стороны равны. | Нет |
| В параллелограмме диагонали точкой пересечения делятся пополам. | Да |
| В параллелограмме есть два равных угла. | Да |
| В параллелограмме противоположные углы равны. | Да |
| Вписанные углы окружности равны. | Нет |
| Вписанные углы, опирающиеся на одну и ту же дугу, равны. | Да |
| Вписанные углы, опирающиеся на одну и ту же хорду окружности, равны. | Нет |
| Вписанный угол измеряется дугой, на которую он опирается. | Нет |
| Вписанный угол измеряется половиной дуги, на которую он опирается. | Да |
| Вписанный угол, опирающийся на диаметр окружности, прямой. | Да |
| Вписанный угол, опирающийся на диаметр окружности, равен 90°. | Да |
| Вписанный угол, опирающийся на полуокружность - развёрнутый. | Нет |
| Вписанный угол равен половине угловой величины дуги, на которую он опирается. | Да |
| Вписанный угол равен половине центрального, опирающегося на туже дугу. | Да |
| В плоскости все точки, равноудалённые от заданной точки, лежат на одной окружности. | Да |
| В плоскости для точки, лежащей вне круга, расстояние до центра круга больше его радиуса. | Да |
| В подобных треугольниках соответствующие стороны равны. | Нет |
| В подобных треугольниках сходственные стороны пропорциональны. | Да |
| В правильном многоугольнике все стороны равны. | Да |
| В правильном многоугольнике все углы равны. | Да |
| В правильном треугольнике все углы прямые. | Нет |
| В прямоугольнике диагонали являются биссектрисами. | Нет |
| В прямоугольнике диагонали являются биссектрисами его углов. | Нет |
| В прямоугольной трапеции основания параллельны. | Да |
| В прямоугольном треугольнике гипотенуза больше катета. | Да |
| В прямоугольном треугольнике гипотенуза меньше катета. | Нет |
| В прямоугольном треугольнике гипотенуза в два раза больше каждого из катетов. | Нет |
| В прямоугольном треугольнике гипотенуза всегда меньше суммы его катетов. | Да |
| В прямоугольном треугольнике гипотенуза равна сумме катетов. | Нет |
| В прямоугольном треугольнике катет больше гипотенузы. | Нет |
| В прямоугольном треугольнике катет, лежащий против угла к 30° равен половине гипотенузы. | Да |
| В прямоугольном треугольнике квадрат гипотенузы равен разности квадратов катетов. | Нет |
| В прямоугольном треугольнике квадрат гипотенузы равен сумме катетов. | Нет |
| В прямоугольном треугольнике любой катет меньше гипотенузы. | Да |
| В прямоугольном треугольнике синус одного из углов равен 0. | Нет |
| В прямоугольном треугольнике тангенсом острого угла а называется отношение sin a / cos a. | Да |
| В равнобедренной трапеции диагонали равны. | Да |
| В равнобедренной трапеции углы при основании равны. | Да |
| В равнобедренном прямоугольном треугольнике все стороны равны. | Нет |
| В равнобедренном прямоугольном треугольнике каждый острый угол равен 45°. | Да |
| В равнобедренном треугольнике все стороны равны. | Нет |
| В равнобедренном треугольнике все углы равны. | Нет |
| В равнобедренном треугольнике имеется не более двух равных углов. | Нет |
| В равнобедренном треугольнике медиана, проведённая к основанию, является одновременно и биссектрисой. | Да |
| В равнобедренном треугольнике медиана, проведённая к основанию, является одновременно и высотой. | Да |
| В равнобедренном треугольнике углы при основании равны. | Да |
| В равностороннем треугольнике АВС медиана AK равна высоте CH. | Да |
| В равностороннем треугольнике все углы острые. | Да |
| В равностороннем треугольнике все углы равны. | Да |
| В равностороннем треугольнике каждый угол равен 45°. | Нет |
| В равностороннем треугольнике медианы пересекаются в одной точке. | Да |
| В ромбе все углы прямые. | Нет |
| В ромбе диагонали пересекаются под прямым углом. | Да |
| В ромбе противоположные углы равны. | Да |
| В ромб нельзя вписать окружность. | Нет |
| Все вписанные углы окружности равны. | Нет |
| Все высоты равностороннего треугольника равны. | Да |
| Все диаметры окружности равны между собой. | Да |
| Все квадраты имеют равные площади. | Нет |
| Все прямоугольные треугольники подобны. | Нет |
| Все прямоугольные треугольники подобны друг другу. | Нет |
| Все равнобедренные треугольники подобны. | Нет |
| Все равнобедренные треугольники равны. | Нет |
| Все точки каждой из двух параллельных прямых равноудалены от другой прямой. | Да |
| Все углы квадрата прямые. | Да |
| Все углы правильного пятиугольника равны 112°. | Нет |
| Все углы правильного шестиугольника равны 135°. | Нет |
| Все углы пятиугольника равны. | Да |
| Все углы ромба равны. | Нет |
| Все хорды одной окружности равны между собой. | Нет |
| Всякий равнобедренный треугольник является остроугольным. | Нет |
| Всякий равносторонний треугольник является остроугольным. | Да |
| Всякий равносторонний треугольник является равнобедренным. | Да |
| В трапеции боковые стороны параллельны. | Нет |
| В трапеции сумма длин боковых сторон всегда меньше суммы оснований. | Нет |
| В трапецию АВCD с основаниями ВС = 7, AD = 10, и боковыми сторонами AB = CD = 8 можно вписать окружность. | Нет |
| В трапецию с основаниями 6 и 3 и боковыми сторонами 4 и 4 можно вписать окружность. | Нет |
| В треугольнике ABC, для которого AB = 3, BC = 4, АС = 5, угол С наименьший. | Да |
| В треугольнике АВС, для которого АВ = 4, BC = 5, AC = 6, угол A наибольший. | Нет |
| В треугольнике АВС, для которого АВ = 4, ВС = 5, АС = 6, угол B — наибольший | Да |
| В треугольнике АВС, для которого АВ = 6, BC = 8, АС = 11, угол при вершине С - наименьший. | Да |
| В треугольнике АВС, для которого ∠A = 40°, ∠B = 60°, ∠C = 80°, сторона AC - наибольшая. | Нет |
| В треугольнике АВС, для которого ∠A = 40°, ∠B = 55°, ∠C = 85° сторона AC - наименьшая. | Нет |
| В треугольнике АВС, для которого ∠A = 44°, ∠B = 55°, ∠C = 81° сторона BC - наибольшая. | Нет |
| В треугольнике АВС, для которого ∠A = 45°, ∠B = 55°, ∠C = 80° сторона AC - наименьшая | Нет |
| В треугольнике АВС, для которого ∠A = 47°, ∠B - 64°, сторона АВ - наибольшая. | Да |
| В треугольнике АВС, для которого ∠A = 50°, ∠B = 60°, ∠C = 70° сторона AB - наибольшая | Да |
| В треугольнике АВС, для которого ∠A = 50°, ∠B = 60°, ∠C = 70° сторона BC - наименьшая. | Да |
| В треугольнике любая сторона меньше суммы двух других сторон. | Да |
| В треугольнике может быть только один тупой угол. | Да |
| В треугольнике против большего угла лежит большая сторона. | Да |
| В треугольнике против большего угла лежит меньшая сторона. | Нет |
| В треугольнике против большей стороны лежит больший угол. | Да |
| В треугольнике против большей стороны лежит меньший угол. | Нет |
| В треугольнике против меньшего угла лежит меньшая сторона. | Да |
| В треугольнике против меньшего угла лежит большая сторона. | Нет |
| В треугольнике против меньшей стороны лежит больший угол. | Нет |
| В треугольнике против меньшей стороны лежит меньший угол. | Да |
| В треугольнике сумма двух сторон больше третьей стороны. | Да |
| В тупоугольном треугольнике все углы тупые. | Нет |
| В тупоугольном треугольнике сумма углов больше 180 градусов. | Нет |
| Высота прямоугольного треугольника, опущенная на гипотенузу, делит его на два подобных треугольника. | Да |
| Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой. | Да |
| Высота равнобедренного треугольника проведённая к основанию, является медианой и биссектрисой. | Да |
| Гипотенуза длиннее катета. | Да |
| Гипотенуза прямоугольного треугольника, вписанного в окружность, в два раза больше её радиуса. | Да |
| Гипотенуза равна сумме квадратов катетов. | Нет |
| Гипотенуза - самая длинная сторона в прямоугольном треугольнике. | Да |
| Два угла с общей стороной называются смежными. | Нет |
| Две окружности пересекаются, если радиус одной окружности больше радиуса другой окружности. | Нет |
| Две прямые всегда пересекаются. | Нет |
| Две прямые, параллельные третьей прямой, перпендикулярны друг другу. | Нет |
| Две прямые, перпендикулярные к третьей, не пересекаются. | Да |
| Две прямые, перпендикулярные одной и той же прямой, не пересекаются. | Да |
| Две прямые, перпендикулярные третьей прямой, параллельны друг другу. | Да |
| Две прямые, перпендикулярные третьей прямой, перпендикулярны друг другу. | Нет |
| Диагонали квадрата взаимно перпендикулярны. | Да |
| Диагонали квадрата делят его углы пополам. | Да |
| Диагонали квадрата пересекаются под прямым углом. | Да |
| Диагонали квадрата равны. | Да |
| Диагонали квадрата точкой пересечения делятся пополам. | Да |
| Диагонали любого прямоугольника делят его на 4 равных треугольника. | Нет |
| Диагонали любого прямоугольника равны. | Да |
| Диагонали параллелограмма делят его углы пополам. | Нет |
| Диагонали параллелограмма пересекаются под прямым углом и в точке пересечения делятся пополам. | Нет |
| Диагонали параллелограмма перпендикулярны. | Нет |
| Диагонали параллелограмма равны. | Нет |
| Диагонали прямоугольника взаимно перпендикулярны. | Нет |
| Диагонали прямоугольника пересекаются под прямым углом и точкой пересечения делятся пополам. | Нет |
| Диагонали прямоугольника равны. | Да |
| Диагонали прямоугольника точкой пересечения делятся пополам. | Да |
| Диагонали прямоугольной трапеции равны. | Нет |
| Диагонали равнобедренной трапеции равны. | Да |
| Диагонали ромба взаимно перпендикулярны. | Да |
| Диагонали ромба в точке пересечения делятся пополам. | Да |
| Диагонали ромба пересекаются под прямым углом. | Да |
| Диагонали ромба пересекаются под углом 60°. | Нет |
| Диагонали ромба перпендикулярны. | Да |
| Диагонали ромба равны. | Нет |
| Диагонали ромба точкой пересечения делятся пополам. | Да |
| Диагонали трапеции пересекаются и делятся точкой пересечения пополам. | Нет |
| Диагонали трапеции пересекаются под прямым углом. | Нет |
| Диагонали трапеции равны. | Нет |
| Диагонали трапеции точкой пересечения делятся пополам. | Нет |
| Диагональ квадрата равна его стороне. | Нет |
| Диагональ параллелограмма делит его на два равных треугольника | Да |
| Диагональ параллелограмма делит его углы пополам. | Нет |
| Диагональ равнобедренной трапеции делит её на два равных треугольника. | Нет |
| Диагональ трапеции делит её на два равных треугольника. | Нет |
| Диагональ трапеции равна квадратному корню из суммы квадратов её оснований. | Нет |
| Диаметр делит окружность на две равные дуги. | Да |
| Диаметр окружности в два раза больше её радиуса. | Да |
| Диаметр окружности в два раза меньше его радиуса. | Нет |
| Длина вектора равна квадратному корню из суммы его координат. | Да |
| Длина вектора, равного сумме двух векторов, не превосходит сумму длин этих векторов. | Нет |
| Длина гипотенузы прямоугольного треугольника больше суммы длин его катетов. | Нет |
| Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов. | Да |
| Длина катета прямоугольного треугольника равна длине гипотенузы, умноженной на косинус угла, образованного этим катетом и гипотенузой. | Да |
| Длина окружности вычисляется по формуле С = 2πR. | Да |
| Длина окружности равна её удвоенному радиусу. | Нет |
| Длина окружности равна πR. | Нет |
| Длина окружности радиуса R равна 2πR. | Да |
| Длина суммы двух векторов равна сумме их длин. | Нет |
| Для любого четырёхугольника, вписанного в окружность, сумма углов, прилежащих к одной стороне, равна 180° | Нет |
|
Для любого числа к и любых векторов а, b справедливо равенство
|
Да |
| Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу. | Да |
| Для точки, лежащей внутри круга, расстояние до центра круга меньше его радиуса. | Да |
| Если в выпуклом четырёхугольнике диагонали перпендикулярны, то этот четырёхугольник - ромб. | Нет |
| Если в параллелограмме две высоты равны, то этот параллелограмм - ромб. | Да |
| Если в параллелограмме две смежные стороны равны, то такой параллелограмм является ромбом. | Да |
| Если в параллелограмме две соседние стороны равны, то такой параллелограмм является ромбом. | Да |