Дан рекурсивный алгоритм. Сколько звездочек напечатае... F(6)?

Задание:

Дан рекурсивный алгоритм:

procedure F(n: integer);
begin
 if n < 3 then
 write('*')
 else begin
 F(n-1);
 F(n-2);
 F(n-2)
 end;
end;
 

Сколько звездочек напечатает эта процедура при вызове F(6)? В ответе запишите только целое число.

Решение:

Решение с помощью дерева:

для n < 3 функция выводит одну звездочку, а для бóльших n продолжаем рисовать дерево

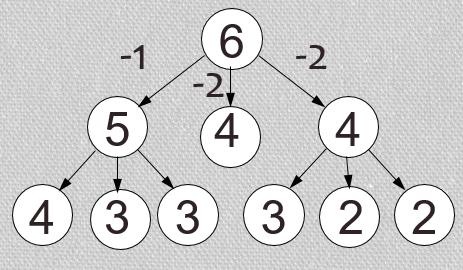
При условии n<3 на экране появляются «звездочки».

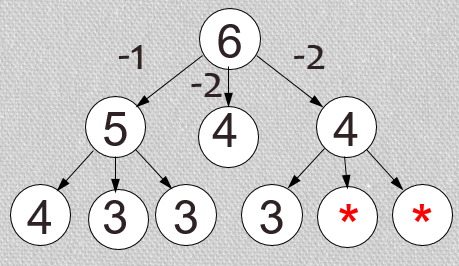
Вторая и третья ветви абсолютно одинаковые, поэтому будем рисовать одну, а количество «звездочек» потом умножим на 2. При условии n<3 на экране появляются «звездочки».

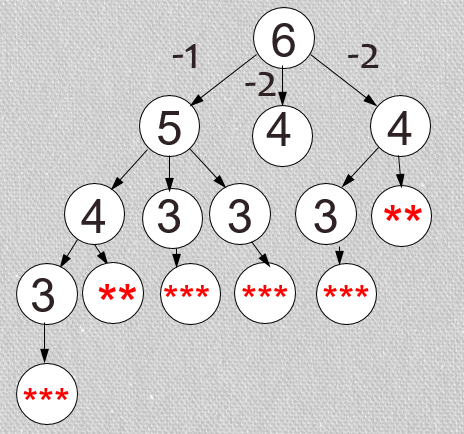
Получаем по первой ветви 11 «звездочек», по третьей, а значит и по второй – по 5. Всего – 21

Решение без дерева:

Пусть S(n) – это количество «звездочек», которые будут выведены при вызове F(n). Тогда

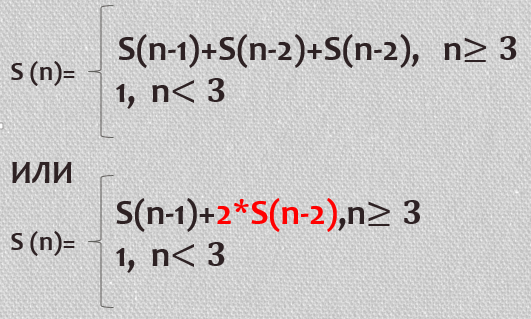
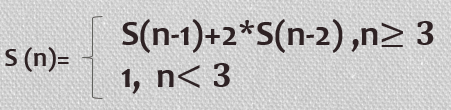
Нам нужно узнать S(6). 
S(6)=S(5)+2*S(4)
S(5)=S(4)+2*S(3)
S(4)=S(3)+2*S(2)
S(3)=S(2)+2*S(0)=S(2)+2*1=S(2)+2
S(2)=1
 

Делаем обратный ход:
S(3)=1+2=3
S(4)=3+2*1=5
S(5)=5+2*3=11
S(6)=11+2*5=21

Ответ: 21