Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками...

Задание:

Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в два раза. Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней.

Игра завершается в тот момент, когда количество камней в куче становится не менее 129. Победителем считается игрок, сделавший последний ход, т.е. первым получивший кучу из 129 или больше камней.
В начальный момент в куче было S камней, 1 ≤ S ≤ 128.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника.
Укажите минимальное значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом.

Решение (аналитическое)

Перед ответом на вопрос задачи определим значения S, при которых Петя может выиграть первым ходом (игра в один ход).
Ходом «добавить в кучу один камень» Петя может выиграть при S = 128.
Ходом «увеличить количество камней вдвое» Петя может выиграть при S ≥ 65.
Объединяя найденные решения, получим, что для игры длиной в один ход выигрышная стратегия есть у первого игрока для значений S ≥ 65.
Теперь исследуем игру в два хода.
Чтобы у второго игрока была возможность выиграть своим первым ходом, первый игрок должен свести игру к одной из позиций, найденных для игры в два хода. Или первый игрок должен однозначно прийти в позицию, где 65 ≤ S ≤ 129.

Ходом «добавить в кучу один камень» первый игрок может прийти в такие позиции только из позиции S = 64. Так как мы ищем значения для выигрышной стратегии второго игрока, значения 65 ≤ S ≤ 129 нас не интересуют, потому что из них первый игрок имеет выигрышную стратегию.

Ходом «увеличить количество камней вдвое» первый игрок придет в позиции для 65 ≤ S ≤ 129 из позиций, где 33 ≤ S ≤ 64.

Теперь найдем позиции, из которых при любом ходе Пети Ваня побеждает.

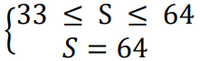
Графически такую игру можно изобразить следующим образом

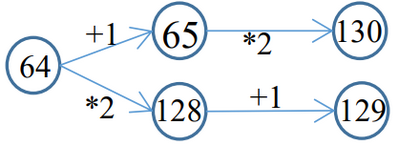
Ответ: 64

Источник: Информатика с Джобсом | ЕГЭ