Исполнитель Чертёжник перемещается на координатной плоскости...
Задание:
Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии.
Чертёжник может выполнять команду сместиться на (a, b), где a, b - целые числа. Эта команда перемещает Чертёжника из точки с координатами (x, y) в точку с координатами (x + a, y + b). Например, если Чертёжник находится в точке с координатами (4, 2), то команда сместиться на (2, -3) переместит Чертёжника в точку (6, -1).
Цикл
ПОВТОРИ число РАЗ
последовательность команд
КОНЕЦ ПОВТОРИ
означает, что последовательность команд будет выполнена указанное число раз (число должно быть натуральным). Чертёжнику был дан для исполнения следующий алгоритм (число повторений и величины смещения в первой из повторяемых команд неизвестны):
НАЧАЛО
сместиться на (4, 6)
ПОВТОРИ ... РАЗ
сместиться на (..., ...)
сместиться на (4, -6)
КОНЕЦ ПОВТОРИ
сместиться на (-28, -22)
КОНЕЦ
В результате выполнения этого алгоритма Чертёжник возвращается в исходную точку. Какое наибольшее число повторений могло быть указано в конструкции «ПОВТОРИ ... РАЗ»?
Аналитическое решение:
Обозначим переменными n, a, b количество итераций цикла и смещение в первой команде тела цикла:
НАЧАЛО
сместиться на (4, 6)
ПОВТОРИ n РАЗ
сместиться на (a, b)
сместиться на (4, -6)
КОНЕЦ ПОВТОРИ
сместиться на (-28, -22)
КОНЕЦ
Для аналитического решения представленной задачи составим систему уравнений, описывающих изменения позиции Чертёжника по осям x и y, равные 0, поскольку исполнитель возвращается в исходную точку:
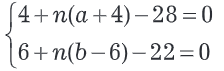
Запишем уравнения системы в виде:
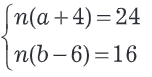
Полученная система уравнений совместна и не определена, т.е. имеет бесконечно много решений. Для целых n, a, b наибольшим значением n является наибольший общий делитель чисел 24 и 16, который равен 8.
Ответ: 8
Проверка в среде Кумир
Для проверки решения в среде Кумир, во-первых, следует вычислить значения переменных a, b для найденного значения n = 8: a = –1, b = 8. Во-вторых, следует записать приведённый в задании алгоритм в среде Кумир с вычисленными значениями переменных n, a, b. Если Чертёжник возвращается в исходную точку и при вычислении максимального количества итераций цикла был корректно вычислен наибольший общий делитель, то был получен правильный ответ (рис. ниже).
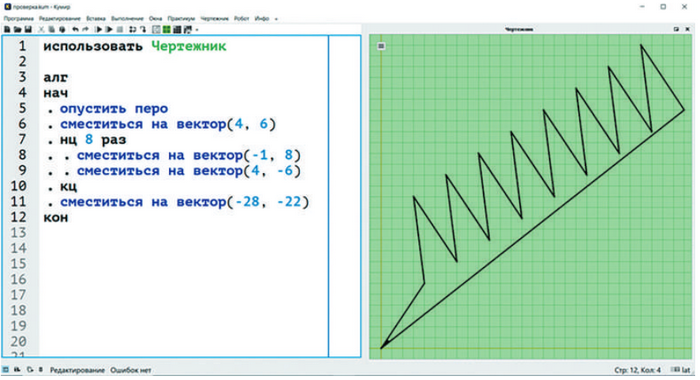
Источник: digital-revolution.ru