Исполнитель Редактор получает на вход строку цифр и преобразовывает...

Задание:

Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.

А) заменить (v, w).
Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Например, выполнение команды
заменить (111, 27)
преобразует строку 05111150 в строку 0527150
Если в строке нет вхождений цепочки v, то выполнение команды заменить (v, w) не меняет эту строку.

Б) нашлось (v).
Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка исполнителя при этом не изменяется.

Цикл
ПОКА условие
    последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ условие
    ТО команда1
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно) или команда2 (если условие ложно).

На выполнение Редактору дана следующая программа:
НАЧАЛО
    ПОКА нашлось (52) ИЛИ нашлось (2222) ИЛИ нашлось (1122)
        ЕСЛИ нашлось (52)
            ТО заменить (52, 11)
        КОНЕЦ ЕСЛИ
        ЕСЛИ нашлось (2222)
            ТО заменить (2222, 5)
        КОНЕЦ ЕСЛИ
        ЕСЛИ нашлось (1122)
            ТО заменить (1122, 25)
        КОНЕЦ ЕСЛИ
    КОНЕЦ ПОКА
КОНЕЦ

На вход приведённой выше программе поступает строка, начинающаяся с цифры «5», а затем содержащая n цифр «2» (3 < n < 10 000).
Определите наибольшее значение n, при котором сумма цифр в строке, получившейся в результате выполнения программы, равна 64.

Решение (аналитическое)

Исследуем работу алгоритма на «бесконечной» строке (n не определено).
522222222222222…
1 итерация:
52 → 11: 1122222222222…
2222 → 5: 115222222222…
2 итерация:
52 → 11: 1111222222222…
2222 → 5: 111152222222…

Можно заметить, что до тех пор, пока в строке перед выполнением команды по замене 2222 на 5 есть 4 или больше двоек, команда по замене 1122 на 25 выполняться не будет.
То есть возможно 4 случая: в конце строки осталось 3 двойки, 2 двойки, 1 двойка или не осталось двоек вовсе. Либо после выполнения алгоритма получается строка вида 111…1115

Проанализируем эти случаи:

3 двойки:
…1111111222 → …11111252 → …11111211 (перед итерацией …111152222)

2 двойки:
…111111122 → …1111125 (перед итерацией …11115222)

1 двойка:
…11111112 не изменится (перед итерацией …1111522)

При отсутствии двоек также изменений не произойдет (перед итерацией …111152).

Чтобы получить строку с суммой цифр 64 алгоритм должен прийти к одному из 5 вариантов:

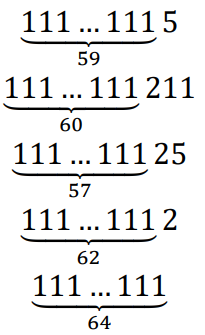
Первый и третий варианты не подходят, так как содержат нечетное количество единиц. Следовательно, остается 3 варианта

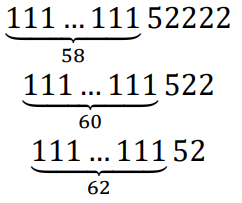
Первый случай получается за 29 итераций, второй - за 30, третий – за 31.
Так как на каждой итерации строка сокращается на 3 символа, то в первом случае она сократилась на 87 символов, во втором – на 90, в третьем – на 93.
Если нам нужна исходная строка максимальной длины, выбираем третий вариант.
То есть длина исходной строки будет 64 + 93 = 157. n = 156.

Ответ: 156

Решение (программное)

Перепишем алгоритм на python и запустим цикл для n от 10 до 20 для обнаружения закономерности.

for n in range(10, 21):
   s = '5' + '2'*n

   while '52' in s or '2222' in s or '1122' in s:
      if '52' in s:
         s = s.replace('52', '11', 1)
         
      if '2222' in s:
         s = s.replace('2222', '5', 1)
               
      if '1122' in s:
         s = s.replace('1122', '25', 1)
   
   print(n, s) 

Получим следующие варианты:

10 11115
11 111111
12 1111112
13 111125
14 1111211
15 1111115
16 11111111
17 111111112
18 11111125
19 111111211
20 111111115
 

Заметим, что с шагом 5 в конечной строке количество единиц в начале строки увеличивается на 2. То есть необходимо найти 5 строк, и которых можно попасть в строки вида 1…15, 1…1, 1…12, 1…125, 1…1211, соответственно, для n имеющего при делении на 5 остатки 0, 1, 2, 3 и 4.
При этом, если получаем строку с суммой цифр больше 64, то запоминаем, что искать следующие строки с большим количеством двоек не имеет смысла (реализуем через счетчик проверенных остатков).

ns = [0]*5
cnt = 0
n = 10

while cnt != 5:
   s = '5' + '2'*n
   while '52' in s or '2222' in s or '1122' in s:
      if '52' in s:
         s = s.replace('52', '11', 1)     

      if '2222' in s:
         s = s.replace('2222', '5', 1)
    
      if '1122' in s:
         s = s.replace('1122', '25', 1)
    
   sm = sum(map(int, s))
   if sm == 64 :
      cnt += 1
      ns[n%5] = n
   elif sm > 64 and ns[n%5] == 0:
      cnt += 1
      ns[n%5] = -1

   n += 1
print(max(ns)) 

Примечание: можно привести менее строгое решение, например, просто увеличив перебор до 1000 (заведомо большое значение) и запомнив все значения n для которых была получена сумма 64.

res = set()
for n in range(10, 1000):
   s = '5' + '2'*n
   
   while '52' in s or '2222' in s or '1122' in s:
      if '52' in s:
         s = s.replace('52', '11', 1)
     
      if '2222' in s:
         s = s.replace('2222', '5', 1)
     
      if '1122' in s:
         s = s.replace('1122', '25', 1)     

   if sum(map(int, s)) == 64 :
      res.add(n)
 
print(max(res))