Между населёнными пунктами А, В, С, D, E... Алгоритм решения

Задание:

Между населёнными пунктами А, В, С, D, E построены дороги, протяжённость которых (в километрах) приведена в таблице. (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.)

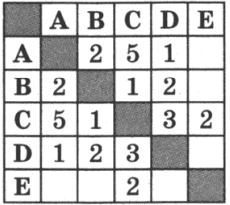
Определите длину кратчайшего пути между пунктами A и E (при условии, что передвигаться можно только по построенным дорогам).

1)4 2)5 3)6 4)7

Решение:

Для решения этой задачи воспользуемся специальным алгоритмом, который эффективно решает именно такого вида задачу — находит кратчайшее расстояние на графе от одной вершины до другой. Этот алгоритм называется алгоритмом Дейкстры. Побочным эффектом алгоритма Дейкстры является нахождение кратчайшего расстояния от некоей стартовой вершины до всех остальных вершин графа. Но это никоим образом не ухудшает его качества — алгоритм Дейкстры ищет кратчайшее расстояние быстро, надежно и эффективно.

0. Выпишем в отдельный список все возможные вершины графа.	A B C D E
1. Будем строить дерево. Нарисуем стартовую вершину (в нашем случае это точка А) и подпишем рядом с ней расстояние, которое нужно «проехать», чтобы добраться до неё из стартовой точки А. То есть, ноль. Эта вершина будет корнем нашего дерева.	А В С D Е А0
2. Из всех возможных листовых вершин дерева найдём вершину с наименьшим числом (в данном случае такая вершина только одна — А). Вычеркнем эту вершину из списка доступных вершин. В дальнейшем её мы больше не будем рассматривать в качестве возможной вершины дерева. То есть, вычеркнутые вершины в дерево больше не дорисовываются! Расстояния до них от стартовой вершины подсчитаны окончательно и лучше уже не будет. Следующее действие будем делать из этой вершины.
3. По таблице расстояний найдём все вершины, до которых идёт ребро из текущей вершины (сейчас это вершина А) и которые ещё не вычеркнуты. Это вершины В, С, D. Нарисуем из текущей вершины (А) ветви дерева для каждой из найденных смежных вершин, нарисуем на концах ветвей названия этих вершин. Подпишем на ветвях длины рёбер по таблице расстояний.
4. Для каждой полученной вершины посчитаем расстояние до неё как: расстояние до текущей вершины (подписано рядом с ней, сейчас для вершины А это 0) плюс расстояние (длина ребра) до каждой полученной вершины (подписано над ребром). Запишем эти расстояния рядом с каждой полученной вершиной.
5. Среди листовых вершин найдём вершину с наименьшим расстоянием. В данном случае это вершина D. Вычеркнем эту вершину из списка доступных вершин. Дальнейшие действия будем делать из неё. Заметим, это такое же действие, как действие 2.
6. По таблице расстояний найдём все вершины, до которых идёт ребро из текущей вершины (сейчас это вершина D) и которые ещё не вычеркнуты. Это вершины В и С. Нарисуем из текущей вершины (D) ветви дерева для каждой из найденных смежных вершин, нарисуем на концах ветвей названия этих вершин. Подпишем на ветвях длины рёбер по таблице расстояний. Заметим, это такое же действие, как действие 3.
7. Для каждой полученной вершины посчитаем расстояние до неё как: расстояние до текущей вершины (подписано рядом с ней, сейчас для вершины D это 1) плюс расстояние (длина ребра) до каждой полученной вершины (подписано над ребром). Запишем эти расстояния рядом с каждой полученной вершиной. Заметим, это такое же действие, как действие 4.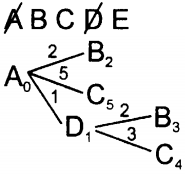
8. Среди всех листовых вершин будем искать одинаковые вершины. Сейчас это пара вершин B2 и B3 и пара вершин C5 и C4. Для каждой пары одинаковых вершин будем вычеркивать в дереве худшую вершину, то есть, вершину с большим расстоянием до неё. Сейчас это B3 и C5. Если в паре одинаковых вершин расстояния будут одинаковые, нужно вычеркнуть одну любую. Мы специально вычеркиваем вершины указанным образом (от левого верхнего к правому нижнему углу), чтобы перечеркнуть как название вершины, так и расстояние до неё. Это облегчит в дальнейшем поиск вершины с наименьшим расстоянием. Заметим, этого действия (вычеркивания) мы раньше не делали, потому что нам ещё не встречались одинаковые вершины. В действительности это часть циклического алгоритма. Действия 5—8 мы будем повторять, пока не вычеркнем конечную вершину из списка доступных вершин.
9. Среди листовых вершин найдём вершину с наименьшим расстоянием. В данном случае это вершина В. Вычеркнем эту вершину из списка доступных вершин. Дальнейшие действия будем, делать из неё.
10. По таблице расстояний найдём все вершины, до которых идёт ребро из текущей вершины (сейчас это вершина В) и которые ещё не вычеркнуты. Это вершина С. Нарисуем из текущей вершины (В) ветви дерева для каждой из найденных смежных вершин, запишем на концах ветвей названия этих вершин. Подпишем на ветвях длины рёбер по таблице расстояний.
11. Для каждой полученной вершины посчитаем расстояние до неё как: расстояние до текущей вершины (подписано рядом с ней, сейчас для вершины В это 2) плюс расстояние (длина ребра) до каждой полученной вершины (подписано над ребром). Запишем эти расстояния рядом с каждой полученной вершиной. Сейчас это C3.
12. Среди всех листовых вершин будем искать одинаковые вершины. Сейчас это C3 и C4. Для каждой пары одинаковых вершин будем вычеркивать в дереве худшую вершину, то есть, вершину с большим расстоянием до неё. Сейчас это C4.
13. Среди листовых вершин найдём вершину с наименьшим расстоянием. В данном случае это вершина С. Вычеркнем эту вершину из списка доступных вершин. Дальнейшие действия будем делать из неё.
14. По таблице расстояний найдём все вершины, до которых идёт ребро из текущей вершины (сейчас это вершина С) и которые ещё не вычеркнуты. Это вершина Е. Нарисуем из текущей вершины (С) ветви дерева для каждой из найденных смежных вершин, запишем на концах ветвей названия этих вершин. Подпишем на ветвях длины рёбер по таблице расстояний.
15. Для каждой полученной вершины посчитаем расстояние до неё как: расстояние до текущей вершины (подписано рядом с ней, сейчас для вершины С это 3) плюс расстояние (длина ребра) до каждой полученной вершины (подписано над ребром). Запишем эти расстояния рядом с каждой полученной вершиной. Сейчас это E5.
16-17. Среди всех листовых вершин будем искать одинаковые вершины. Сейчас таких пар нет. Среди листовых вершин найдём вершину с наименьшим расстоянием. В данном случае это вершина E. Вычеркнем эту вершину из списка доступных вершин. Это конечная вершина, расстояние до которой мы искали. Алгоритм закончен. Кратчайшее расстояние — 5. Ответ: 5