На числовой прямой даны три отрезка: P = [10,15], Q = [10,20]...

Задание:

На числовой прямой даны три отрезка: P = [10,15], Q = [10,20] и R=[5,15]. Выберите такой интервал A, что формулы (x ∈ A) → (x ∈ P) и (x ∈ Q) → (x ∈ R) тождественно равны, то есть принимают равные значения при любом значении переменной х (за исключением, возможно, конечного числа точек).

1) [5, 12]
2) [10, 17]
3) [12, 20]
4) [15, 25]

Решение:

Преобразуем выражения:

(x ∈ A) → (x ∈ P) = (x ∉ A) V (x ∈ P)
(x ∈ Q) → (x ∈ R) = (x ∉ Q) V (x ∈ R)

Затем построим две прямые, и отметим на каждой свои промежутки.

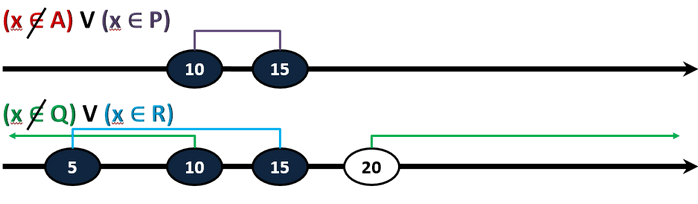
Вторая функция принимает значение единица везде, кроме промежутка (15,20]. У нас в выражении фигурирует промежуток, обратный промежутку А. Нужно выбрать такой промежуток А, обратный которому не должен перекрывать промежуток (15,20], но должен перекрыть все остальные неперекрытые значения.

1) [5, 12] - обратный (-∞,5)U(12, ∞) – включает промежуток (15,20]
2) [10, 17] - обратный (-∞,10)U(17, ∞) – включает часть промежутка (15,20]
3) [12, 20] - обратный (-∞,12)U(20, ∞) – подходит
4) [15, 25] - обратный (-∞,15)U(25, ∞) – не перекрывает диапазон значений (20,25]

Ответ: 3