Найдите наименьшее ... у = 2х3 + 9х2 - 60х + 5...

Задание:

Найдите наименьшее значение функции у = 2х³ + 9х² - 60х + 5 на отрезке [-1,5; 11].

Решение:

Найдём производную исходной функции: y'(x) = 6x² + 18x − 60.

Найдём нули производной из уравнения y'(x) = 0; 6x² + 18x − 60 = 0; x² + 3x − 10 = 0,

x_1,2 =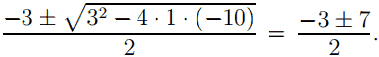

 Отсюда x₁ = −5, x₂ = 2. Расставим знаки производной и определим промежутки монотонности исходной функции.

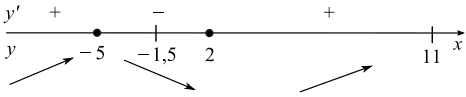
Из рисунка видно, что функция y = 2x³+ 9x² − 60x + 5 убывает на промежутке [−1,5; 2] и возрастает на промежутке [2; 11]. Значит, на промежутке [−1,5; 11] наименьшее значение достигается при x = 2 и равно y(2) = 2·2³ + 9·2² − 60·2 + 5 = 16 + 36 −120 + 5 = −63.

Ответ: −63.