Найдите точку максимума функции y = ln(x + 4)^2 + 2x + 7...
Задание:
Найдите точку максимума функции y = ln(x + 4)2 + 2x + 7.
Решение:
Честно считаем производную, приравниваем её к нулю, находим стационарные точки – корни уравнения, среди этих точек ищем точки максимума – проходя через них производная меняет знак с плюса на минус. Отметим, что х = –4 не является допустимым значением аргумента (ОДЗ).
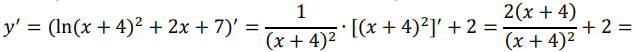
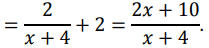
Единственный корень уравнения у' = 0 это x = –5.
Ответ: -5