Найдите точку минимума функции y = (6 - 4x)  * cos x...

Задание:

Найдите точку минимума функции y = (6 - 4x)  * cos x + 4 sin x + 14, принадлежащую промежутку (0; π/2).

Решение:

Найдем производную заданной функции:

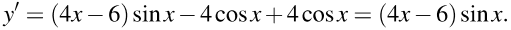
На заданном промежутке синус не обращается в нуль и принимает только положительные значения.

4x - 6 = 0
4x = 6
x = 6/4
x = 1.5

Поэтому единственный нуль производной — число 1,5.

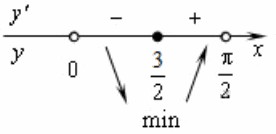
Определим знаки производной функции: она положительна при x < 1,5 и отрицательна при x > 1,5. Поэтому искомая точка минимума — число 1,5.

Искомая точка минимума: x = .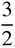

Ответ: 1,5.