Найдите ... у = (х + 4)^2(х + 1) + 19 на отрезке [-5; -3].

Задание:

Найдите наибольшее значение функции у = (х + 4)²(х + 1) + 19 на отрезке [-5; -3].

Решение:

Найдём производную исходной функции, используя формулу производной произведения:

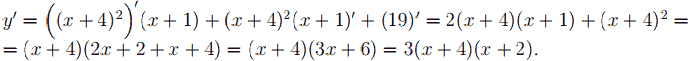Отыщем нули производной: y'(x) = 0; (x + 4)(x + 2) = 0; x₁ = −4, x₂ = −2. Рас- ставим знаки производной и определим промежутки монотонности исходной функции. Из рисунка видно, что на отрезке [−5; −4] исходная функция возрастает, а на отрезке [−4; −3] убывает.

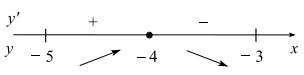
Таким образом, наибольшее значение на отрезке [−5; −3] достигается при
x = −4 и равно y(−4) = (−4 + 4)²(−4 + 1) + 19 = 19.

Ответ: 19.