Операнды арифметического выражения записаны в системе счисления...

Задание:

Операнды арифметического выражения записаны в системе счисления с основанием 19.

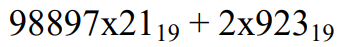
В записи чисел переменной x обозначена неизвестная цифра из алфавита 19-ричной системы счисления. Определите наибольшее значение x, при котором значение данного арифметического выражения кратно 18.
Для найденного x вычислите частное от деления значения арифметического выражения на 18 и укажите его в ответе в десятичной системе счисления. Основание системы счисления указывать не нужно.

Решение (аналитическое)

Воспользуемся тождествами модульной арифметики:

(a + b) mod D = (a mod D + b mod D) mod D,
(a ∙ b) mod D = ((a mod D) ∙ (b mod D)) mod D,

где mod – операция взятия остатка от деления
Исследуем с помощью этих тождеств степени предложенного основания числа

19 mod 18 = 1
19² mod 18 = 1∙1 mod 18 = 1
19³ mod 18 = 1∙1 mod 18 = 1
… 
19ⁿ mod 18 = 1

Теперь представим предложенные числа с учетом этого наблюдения

((9∙1 + 8∙1 + 8∙1 + 9∙1 + 7∙1 + x∙1 + 2∙1 + 1∙1) + (2∙1+x∙1+9∙1+2∙1+3∙1)) mod 18 = 0
((9 + 8 + 8 + 9 + 7 + x + 2 + 1) + (2+x+9+2+3)) mod 18 = 0

Или можем свести задачу к следующей «найти значение x, при котором сумма разрядов двух чисел кратна 18.

(60 + 2x) mod 18 = 0
(6 + 2x) mod 18 = 0
x ∈ {6, 15}
x_max = 15

Теперь представим полеченное выражение в виде степенного ряда и вычислим искомое частное. Вычисления будем проводить в калькуляторе или среде программирования.

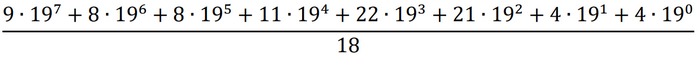
Ответ: 469034148

Решение (программное)

for x in '0123456789abcdefghi'[::-1]:
   sm = int(f'98897{x}21', 19) + int(f'2{x}923', 19)
   if sm % 18 == 0:
      print(sm // 18)
      break 

Или можем решить задачу в числовом виде

def num(*ds):
   ds = ds[::-1]
   return sum(ds[i]*19**i for i in range(len(ds)))

for x in range(18, -1, -1):
   sm = num(9,8,8,9,7,x,2,1) + num(2,x,9,2,3)
   if sm % 18 == 0:
      print(sm // 18)
      break 

Ответ: 469034148

Источник: Информатика с Джобсом | ЕГЭ