Укажите через запятую в порядке возрастания все основания...

Задание:

Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 71 оканчивается на 13.

Решение:

Минимально возможная система счисления – 4, так как у нас есть цифра 3. Пусть основание искомой системы = x, тогда

x² * c + 1 * x¹ + 3 * x⁰ = 71, где с – натуральное число, либо 0.

Зная, что x⁰=1, x¹ = x, получим  x² * c + x + 3 = 71

Отсюда

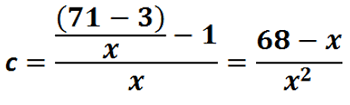
Чем больше x, тем меньше с, поэтому значения с не превышают (68 - 4) / (4 * 4) = 4. Переменная с [0..4]

Получаем:
а) при c = 0, x = 68.
б) при c = 1, 2, 3 решения — не целые числа;
в) при c = 4, x₁ = 4 и  x₂ = -4.25 условию натуральности соответствует только первое решение.

Ответ: 4, 68