15-го января планируется взять кредит в банке...

Задание:

15-го  января  планируется  взять  кредит  в  банке  на  шесть  месяцев  в размере  1  млн  рублей. 
Условия его возврата таковы: 
- 1-го  числа  каждого  месяца  долг  увеличивается  на  r  процентов  по  сравнению  с  концом предыдущего месяца, где r – целое число; 
-  со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; 
- 15-го  числа  каждого  месяца  долг  должен  составлять  некоторую  сумму  в  соответствии  со следующей таблицей. 

Найдите  наибольшее  значение  r,  при  котором  общая  сумма  выплат будет  меньше  1,2 млн рублей. Решение.

Решение:

По  условию,  долг  перед  банком  (в  млн  рублей)  на  15-е  число  каждого месяца  должен уменьшаться до нуля следующим образом: 1; 0,6; 0,4; 0,3; 0,2; 0,1; 0.

Пусть   k = 1 + r / 100, тогда долг на 1-е число каждого месяца равен: 
k; 0,6k; 0,4k; 0,3k; 0,2k; 0,1k. 

Следовательно, выплаты со 2-го по 14-е число каждого месяца составляют: 

k - 0.6; 0.6k - 0.4; 0.4k - 0.3; 0.3k - 0.2; 0.2k - 0.1; 0.1k

Общая сумма выплат составляет: 

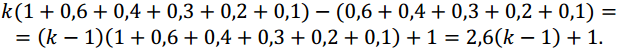
По условию, общая сумма выплат будет меньше 1,2 млн рублей, значит,

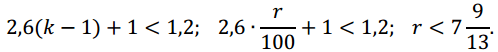
Наибольшее целое решение этого неравенства – число 7. Значит, искомое число процентов – 7.

Ответ: 7.