Из пункта A в пункт B, расположенный ниже по...

Задание:

Из пункта A  в пункт B,  расположенный ниже по течению реки, отправился плот. Одновременно с этим из пункта B в пункт A вышел катер, собственная скорость которого в шесть раз больше скорости течения реки.  Встретив плот,  катер сразу повернул и  поплыл обратно.  Какую часть расстояния от пункта А до пункта В останется проплыть плоту к тому моменту, когда катер вернётся в пункт В?

Решение:

Пусть v — скорость течения реки,  t — время, прошедшее с момента отплытия плота и катера до момента их встречи. Тогда скорость катера при движении от пункта B навстречу плоту равна  6v - v  = 5v  (собственная скорость  катера,  которая  в  6 раз  больше  скорости  течения,  минус  скорость течения).

За время  t  плот проплывёт расстояние  vt ,  а катер — расстояние 5vt. Поэтому расстояние между пунктами A и B равно  vt + 5vt = 6vt.

После встречи с плотом катер плывёт обратно то есть вниз по течению, и его скорость равна  6v + v = 7v (собственная скорость катера плюс скорость течения).  Поэтому расстояние от места встречи с плотом до пункта B, равное 5vt, катер проплывет за время .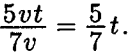

За время 5t/7 плот проплывает расстояние 5t/7 * v, а общее расстояние, пройденное плотом к моменту возвращения катера в пункт B, будет равно 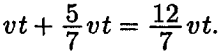. Следовательно, к моменту возвращения катера в пункт B плоту останется проплыть расстояние, равное  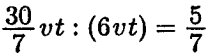,  что составляет  (рисунок)  частей всего расстояния от A до B.

Ответ: 5/7