Линейно зависимы ли векторы в R^4? a1 = (4, −5, 2, 6)...
Задание:
Линейно зависимы ли векторы в R4?
a1 = (4, −5, 2, 6), a2 = (2, −2, 1, 3), a3 = (6, −3, 3, 9), a4 = (4, −1, 5, 6).
Решение:
Составим линейную комбинацию векторов a1, a2, a3, a4:
α1a1 + α2a2 + α3a3 + α4a4.
Чтобы выяснить, являются ли векторы a1, a2, a3, a4 линейно зависимыми или нет, достаточно определить, сколько решений имеет уравнение
α1a1 + α2a2 + α3a3 + α4a4 = 0, где в качестве неизвестных выступают коэффициенты α1, α2, α3, α4. Если это уравнение имеет единственное решение (нулевое решение есть всегда), то векторы линейно независимы. Если у уравнения есть ненулевое решение, то векторы линейно зависимы.
Подставим числовые значения векторов a1, a2, a3, a4, получим:
α1(4, −5, 2, 6) + α2(2, −2, 1, 3) + α3(6, −3, 3, 9) + α4(4, −1, 5, 6) = (0, 0, 0, 0).
Умножим каждый из векторов на свой коэффициент и сложим все векторы в левой части равенства, получим:
(4α1 + 2α2 + 6α3 + 4α4, −5α1 − 2α2 − 3α3 − α4, 2α1 + α2 + 3α3 + 5α4, 6α1 + 3α2 + 9α3 + 6α4) = (0, 0, 0, 0).
Два вектора равны, если равны их соответствующие компоненты. Следовательно полученное равенство векторов равносильно системе:
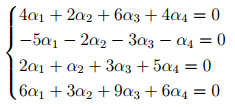
Найдем число решений этой системы, используя метод Гаусса. Матрица коэффициентов имеет вид:
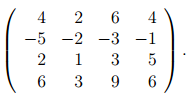
Заметим, что столбцы матрицы коэффициентов — это в точности данные четыре вектора. Мы не пишем столбец со свободными членами, так как все они равны нулю и при элементарных преобразованиях строк не меняются. Приведем матрицу к ступенчатому виду:
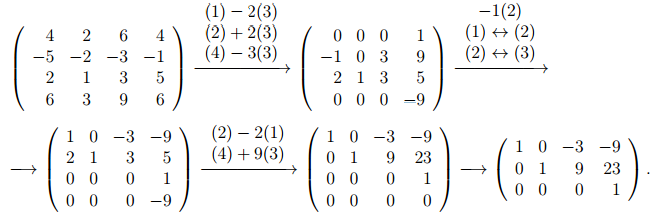
Полученная матрица состоит из трех строк и четырех столбцов. Исходная система линейных уравнений имеет ненулевое решение. Следовательно данные векторы a1, a2, a3, a4 линейно зависимы.
Ответ. Векторы a1, a2, a3, a4 линейно зависимы.
