Найдите наименьшее значение функции y = 5cos x...

Задание:

Найдите наименьшее значение функции y = 5cos x - 6x + 4 на отрезке [-3пи/2;0]

Решение:

Сначала найдем значения функции на концах отрезка:

y[0] = 5cos 0 - 6 * 0 + 4 = 5 + 4 = 9

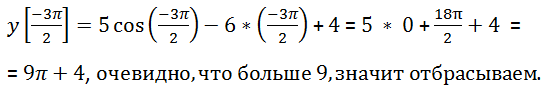
Функция принимает наибольшее или наименьшее значение там, где производная равна нулю:

Найдем производную и приравняем ее к нулю.

y* = -5sin x - 6
-5sin x - 6 = 0
-5sin x = 6
sin x = -6/5 - корней нет, так как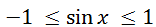 

Ответ: 9