Найдите площадь треугольника, вершины...

Задание:

Найдите площадь треугольника (в см²), вершины которого имеют координаты (4; 2), (6; 2), (4;10).

Решение:

Способ 1:

Площадь прямоугольного треугольника равна половине произведения его катетов. Найдём длину катета BA.Абсцис­сы (х) у них равны. Находим разность ординат (у),длина AB

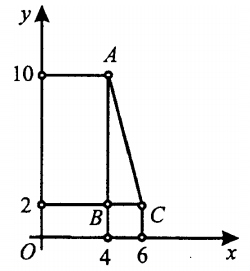
равна 10 - 2 = 8. Длину отрезка BC,параллельного оси Ох, можно найти, если вычесть их абсциссы: 6 - 4 = 2.

Тогда площадь S = (2 * 8) / 2 = 8 (см²)

Способ 2:

Нанесём координатную сетку (нарисуем линии с промежутком 1 прямо на данном чертеже.

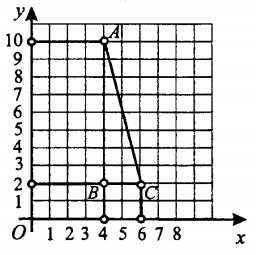
После этого по клеточкам посчитаем длину катетов и вычислим площадь. AB= 8, BC = 2.

S = (2 * 8) / 2 = 8 (см²)

Ответ: 8