Найдите точку минимума функции у = 2х^3 + З6х^2 +...

Задание:

Найдите точку минимума функции у = 2х³ + З6х² + 162х + 57.

Решение:

Найдём производную исходной функции: y'(x) = 6x² + 72x + 162.

Найдём нули производной из уравнения

y'(x) = 0;

6x² + 72x + 162 = 0;

x² + 12x + 27 = 0,

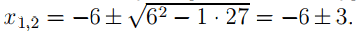
Отсюда x₁ = −9, x₂ = −3. Расставим знаки производной и определим промежутки монотонности исходной функции. Из рисунка видно, что значение x = −3 является единственной точкой минимума.

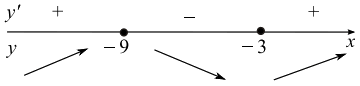
Ответ: -3.