Прямая 3x + 4y = c, где c - некоторое число...

Задание:

Прямая  3x + 4y = c,  где  c - некоторое число, касается гиперболы y = 12/x  в точке с отрицательной абсциссой. Найдите число с.

Решение:

1)  Изобразим прямую  3x+ 4y = 0  и график функции у = 12/x.
   

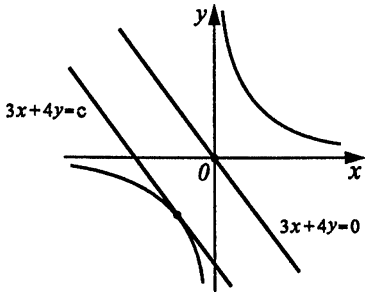
Прямые  3x + 4y = с  и  3x + 4y = 0  параллельны при любом значении  c. Поэтому на  основании рисунка делаем вывод, что прямая  3x + 4y =  с касается графика  у  =  12/x в том  и только том случае,  когда она имеет с этим графиком ровно одну общую точку.

2)  Прямая  3x + 4y  =  c  и график  у = 12/x имеют ровно одну общую точку тогда и только тогда, когда система уравнений 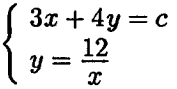  имеет ровно одно решение.

Подставляя  y =  12/x  в первое уравнение системы, получаем: 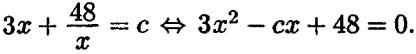. Каждому корню x₀ уравнения 3x² — cx + 48 = 0 соответствует ровно одно решение x = x₀,  y =  12/x  указанной выше системы, и наоборот.
Уравнение  3x² — cx + 48  =  0 имеет единственный корень (x₀ = с/6) в том и только в том случае, когда его дискриминант D = c² - 12 * 48 равен нулю.

На основании изложенного выше получаем, что прямая  Зx + 4y = c касается графика  у = 12/x тогда и только тогда, когда c² — 12 * 48 = 0,  c²  = 12² * 4,  c = ±24. 
Так как по условию абсцисса точки касания  x₀ =  c/6  отрицательна, то c < 0, то есть  c =  -24.

Ответ: c = -24