В геометрической прогрессии сумма первого...

Задание:

В геометрической прогрессии сумма первого и второго членов равна 1000, а сумма первых четырёх членов равна 1010. Найдите сумму первых восьми членов этой прогрессии, если известно, что её знаменатель положителен.

Решение.

Пусть b - первый член данной в условии геометрической прогрессии, q - знаменатель этой прогрессии. Тогда b * q, b * q², b * q³ - второй, третий и четвёртый члены этой прогрессии. По условию имеем:

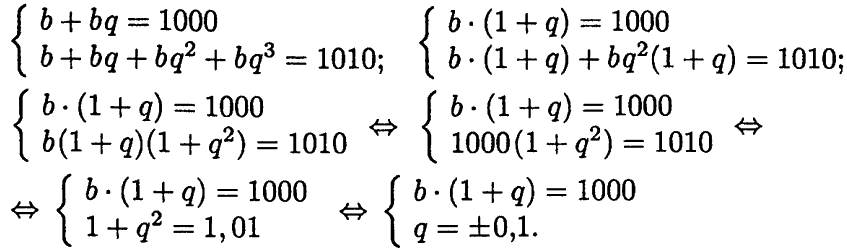
Так как по условию q > 0, то q = 0,1. Чтобы вычислить сумму первых восьми членов прогрессии заметим, что b₅ + b₆ + b₇ + b₈ = bq⁴ + bq⁵ + bq⁶ + bq⁷ = q⁴(b + bq + bq² + bq³) = q⁴ * 1010 = 1010 * 0,1⁴: 0,101. Поэтому сумма первых восьми членов равна 1010 + 0,101 = 1010,101.

Ответ: 1010.101