В трапеции ABCD, в которой AD || ВС, точка О — точ...

Задание:

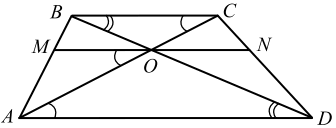
В трапеции ABCD, в которой AD || ВС, точка О — точка пересечения диагоналей трапеции. Через эту точку проведена прямая, параллельная основаниям и пересекающая боковые стороны в точках М и N.

а) Докажите, что МО = ON.

б) Найдите отношение если BC/AD, если BD/OB = 5/2.

Решение:

а) 1. ΔAOD ∼ ΔBOC (по двум углам: ∠BCO = ∠CAD как накрест лежащие при параллельных прямых AD и BC и секущей AC, ∠CBO = ∠ODA как накрест лежащие при параллельных прямых AD и BC и секущей BD).

Отсюда следует, что BO / OD = OC / AO. Тогда BO/OD + 1 = OC/AO + 1, (BO + OD) / OD = (OC + AO) / AO , BD / OD = AC / AO. (1)

2. ΔABC ∼ ΔAMO (по двум углам: ∠BCA = ∠MOA, ∠BAC — общий). Следовательно, BC / MO = AC / AO. (2)

Аналогично ΔDBC ∼ ΔDON ⇒ BC / ON = BD / OD . С учётом (1), получим:

BC / ON = AC / AO. Из этого равенства, с учётом (2), получим: BC / ON = BC / MO . Следовательно, ON = MO.

б) BC / AD = BO / OD = BO / (BD − BO) , AD / BC = (BD − BO) / BO = BD/BO − 1 = 5/2 − 1 = 3/2 . Тогда BC / AD = 2 / 3 .

Ответ: 2/3.