Все рёбра правильной треугольной призмы АВСА1...
Задание:
Все рёбра правильной треугольной призмы АВСА1В1С1 имеют длину 6. Точки M и N – середины рёбер АА1 и А1С1 соответственно. а) Докажите, что прямые ВМ и MN перпендикулярны.
б) Найдите угол между плоскостями BMN и АВВ1.
Решение:
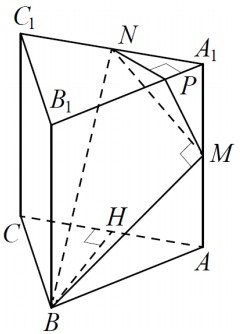
а) Пусть точка Н – середина АС. Тогда
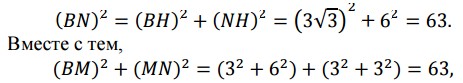
а тогда по теореме, обратной теореме Пифагора, треугольник BMN является прямоугольным с прямым углом М.
б) Проведём перпендикуляр NP к прямой А1В1. Тогда NP ⊥ А1В1 и NP ⊥ А1А. Следовательно, угол NMP – линейный угол искомого угла.
Длина NP равна половине высоты треугольника А1В1С1, то есть 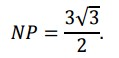
Поэтому
