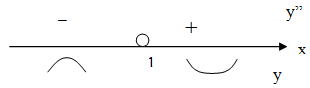Исследование функции и построение ее графика

Исследование функции и построение ее графика

1). Если f'(x) > 0  внутри промежутка I, то функция f возрастает на промежутке I.
2). Если f'(x) < 0  внутри промежутка I, то функция f убывает на промежутке I.

Если в точке x₀ производная меняет знак с «+» на « - », то x₀ – точка максимума.
Если в точке x₀ производная меняет знак с « - » на « + », то x₀ – точка минимума.

Пример № 1. Для кривой y = 3x²  - 6x  + 5   найти интервалы монотонности и точки экстремума.

Решение.
1). Находим производную функции:  y' = (3x²  - 6x  + 5)' = 6x - 6
2).  Определим промежутки возрастания и убывания функции:

6x - 6 > 0 ; 
6x - 6 < 0; 
6x - 6 = 0
6x = 6
x = 1

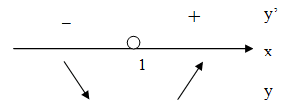
x = 0; y’= 0 – 6 =– 6 ( – )
x = 2; y’= 12 – 6 = 6  ( + )

Ответ:  у возрастает при  x ∈ (1; +∞); у убывает при x ∈ (-∞; 1)  Точка минимума: (1; 2) , т.к. при x = 1; y = 3 * 1² - 6 * 1 + 5 = 2.

1). Если f''(x) > 0  внутри промежутка I, то функция f вогнута на промежутке I.
2). Если f''(x) < 0   внутри промежутка I, то функция f выпукла на промежутке I.
Обращаем ваше внимание на вторую производную функции.

Если в точке x₀ вторая производная меняет знак с «+» на « - » или с « - » на « + »,, то x₀ – точка перегиба функции.

Пример № 2. Для кривой  y =  (1/3)x³ – x²   найти промежутки выпуклости и точки перегиба.
Решение.    
1)    Находим вторую производную функции:

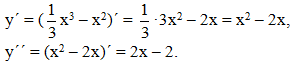
2) Определим промежутки выпуклости:

2x - 2 > 0;
2x - 2 < 0;
2x - 2 = 0;
2x = 2
x = 1