Из пункта A в пункт B одновременно выехали два...

Задание

Из пункта A в пункт B одновременно выехали два автомобилиста. Первый проехал с постоянной весь путь. Второй ехал первую половину пути со скоростью, меньшей скорости первого на 7 км/ч, а вторую половину пути - со скорость 72 км/ч, в результате прибыл в B одновременно с первым автомобилистом. Найдите скорость первого автомобилиста, если известно, что она больше 30 км/ч. Ответ дайте в км/ч.

Решение:

Пусть скорость первого автомобилиста равна x км/ч - ее нам нужно найти, тогда скорость второго автомобилиста в первой половине пути равна x - 7; За расстояние примем 1 км.

Для первого автомобилиста:

s = x * t

Для второго автомобилиста:

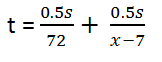
Приравняем уравнения, так как известно, что они прибыли в точку B одновременно:

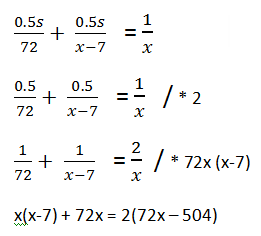
x² - 7x + 72x = 144x - 1008
x² + 65x - 144x + 1008 = 0
x² - 79x + 1008 = 0

Решаем квадратное уравнение по теореме Виета или по дискриминанту и получаем:

x = 63 - удовлетворяет условию задачи x > 30
x = 16 - не удовлетворяет условию задачи x > 30

Ответ: 63