Касательные к окружности с центром O в точках A и B...

Задание:

Касательные к окружности с центром O в точках A и B пересекаются под углом 72º. Найдите угол ABO.

Решение:

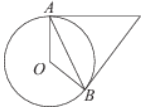
Пусть касательные пересекаются в точке M. Отрезки касательных, проведенных из одной точки равны:

AM = MB, значит треугольник AMB – равнобедренный. По свойству равнобедренного треугольника ∠MBA = 

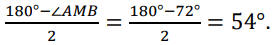
Так как радиус, проведенный в точку касания перпендикулярен касательной, то ∠OBM = 90° ⇒ ∠ABO = 90° − 54° = 36°.

Ответ: 36