Найдите площадь закрашенной фигуры на координатной плоскости...

Задание:

Найдите площадь закрашенной фигуры на координатной плоскости.

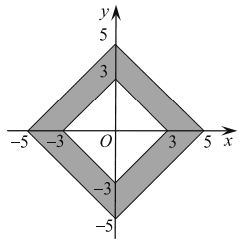
Решение:

Площадь закрашенной фигуры равна разности площади большого квадрата и маленького квадрата. Поэтому:

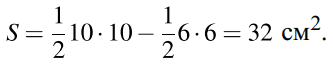
Способ 2: Большой квадрат разбит на 4 прямоугольных треугольника. Найдем гипотенузу, которая является стороной квадрата:

Гипотенуза C² = 5² + 5²

C² = 50
С = √50 - сторона большего квадрата.
Площадь большего квадрата = длину умножить на ширину = √50 * √50 = 50 (ед²)

Аналогично с маленьким квадратом. Найдем гипотенузу, которая является стороной квадрата:

Гипотенуза C² = 3² + 3²

C² = 18
С = √18 - сторона большего квадрата.
Площадь маленького квадрата = длину умножить на ширину = √18 * √18 = 18 (ед²)

Площадь закрашенной фигуры равна разности площади большого квадрата и маленького квадрата. Поэтому: S = 50 - 18 = 32 (ед²)

Ответ: 32.