Основание АС равнобедренного треугольника АВС равно 12...

Задание:

Основание АС равнобедренного треугольника АВС равно 12. Окружность радиуса 8 с центром вне этого треугольника касается продолжений боковых сторон треугольника и касается основания АС. Найдите радиус окружности, вписанной в треугольник АВС.

Решение:

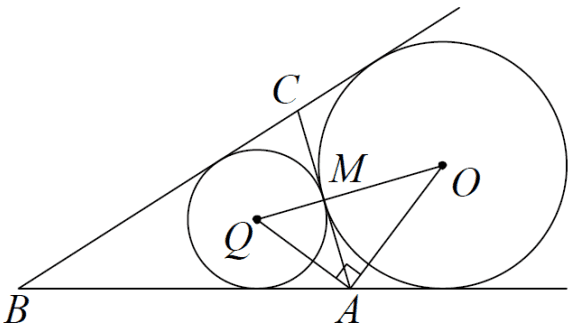
Пусть О – центр данной окружности (она называется вневписанной), а Q – центр вписанной окружности треугольника АВС. Точка касания М этих окружностей делит АС пополам (биссектриса, проведенная к основанию, также и медиана).

AQ и АО – биссектрисы смежных углов, значит угол OAQ – прямой. Из прямоугольного треугольника OAQ получаем:

(AM)² = (QM) * (MO)

квадрат высоты прямоугольного треугольника равен произведению проекций катетов на гипотенузу (выводится из подобия треугольников, на которые высота разбивает данный прямоугольный треугольник). В таком случае:

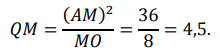
Ответ: 4.5