Первый велосипедист выехал из посёлка по шоссе со скоростью...

Задание:

Первый велосипедист выехал из посёлка по шоссе со скоростью 18 км/ч. Через час после него со скоростью 16 км/ч из того же посёлка в том же направлении выехал второй велосипедист, а ещё через час — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 4 часа после этого догнал первого.

Решение:

Пусть скорость третьего велосипедиста равна v км/ч, а t ч — время, за которое он догнал второго велосипедиста. Начало отсчёта времени — момент, когда первый велосипедист начал движение. Тогда за время t третий велосипедист догонит второго, и к данному моменту второй велосипедист проедет расстояние (16t - 1) км, а третий — расстояние v(t - 2) км. Аналогично за время (t + 4) третий велосипедист догонит первого, и к этому моменту первый велосипедист проедет 18(t + 4) км, а третий —  v(t + 4 - 2) км. Составим систему уравнений: 

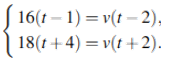
Умножим первое уравнение на t + 2,  а второе — на t - 2 и вычтем первое уравнение из второго:

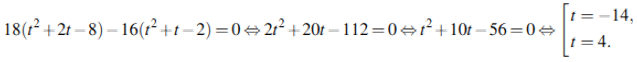
По условию задачи подходит только положительный корень, то есть t = 4 Подставляя t во второе уравнение найдём

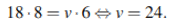
Ответ: 24