Постройте график функции y = x2 - |6x + 5|. Определите, при каких...

Постройте график функции y = x² - |6x + 5|.
Определите, при каких значениях m прямая y = m имеет с графиком ровно три общие точки.

Решение:

Раскроем модуль и составим систему уравнений:

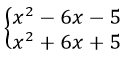
1) y = x2 - 6x - 5
D = (-6)² - 4 * 1 * (-5) = 56 = (2√14)²
x₁ = (6 + 2√14) / 2 = 3 + √14
x₂ = (6 - 2√14) / 2 = 3 - √14
x_{вершины} = - b / 2a = 6 / 2 = 3
y_{вершины} = 9 - 18 - 5 = -14
2) y = x2 + 6x + 5
D = 6² - 4 * 1 * 5 = 16
x₁ = (-6 + 4) / 2 = -1
x₂ = (-6 - 4) / 2 = -5
x_{вершины} = - b / 2a = -6 / 2 = -3
y_{вершины} = 9 - 18 + 5 = -4

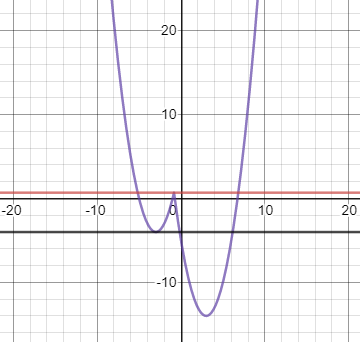
Как видно по графику, прямая y = m имеет с функцией ровно три общие точки в случае y = -4 и в случае прямой проходящей через точку пересечения двух графиков.

Найдем точку пересечения:
x² - 6x - 5 = x² + 6x + 5
-12x = 10
x = -10 / 12 = -5 / 6
y = x² - 6x - 5 = (-5 / 6)² - 6 * (-5 / 6) - 5 = 25/36 + 5 - 5 = 25/36
Во втором случае m = 25 / 36.

Ответ: m = -4, m = 25/36.