Прямая касается окружности в точке K. Точка O — центр окружности...

Задание:

Прямая касается окружности в точке K. Точка O — центр окружности. Хорда KM образует с касательной угол, равный 83º. Найдите величину угла OMK. Ответ дайте в градусах.

Решение:

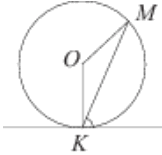
Так как радиус, проведенный в точку касания перпендикулярен касательной, то ∠OKM = 90° − 83° = 7°. 
Треугольник KOM - равнобедренный, так как КO = MO – радиусы окружности.
По свойству равнобедренного треугольника ∠OMK = ∠OKM = 7°.

Ответ: 7