Решите неравенство 1 / (1 + 2^х) - 2 / (4^х - 2х + 1) < ...
Категория: Задание 15 ЕГЭ по математике (Неравенства)
Задание:
Решите неравенство 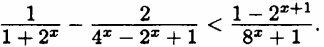
Решение:
С помощью замены 2 x = t, где t > 0, приведём неравенство к виду
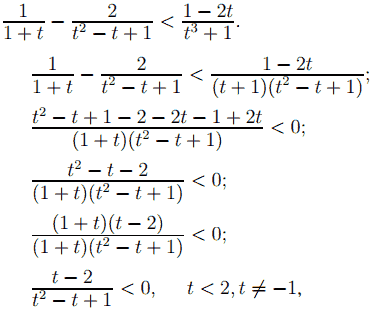
Учитывая условие t > 0, имеем 0 < t < 2. Возвращаясь к переменной x, получим, что 0 < 2x < 2, откуда x < 1.
Ответ: (−∞; 1).