Решите неравенство 9^x - 2 * 3^(x+1)...
Категория: Задание 15 ЕГЭ по математике (Неравенства)
Задание:
Решите неравенство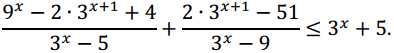 
Решение:
Пусть t = 3x , тогда неравенство примет вид:
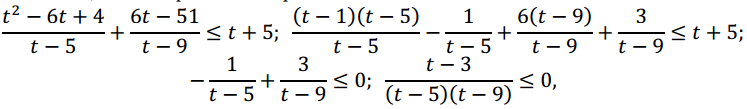Откуда t ≤ 3; 5 < t < 9.
При t ≤ 3 получим: 3x ≤ 3 , следовательно x ≤ 1
При 5 < t < 9 получим: 5 < 3x < 9, следовательно log35 < x < 2.
Решение исходного неравенства: x ≤ 1 и log35 < x < 2.
Ответ: (-∞;1] (log35;2)