Решите неравенство (7х - 10) log4х - 3(x^2 - 4х + 9) ≥ 0.

Задание:

Решите неравенство (7х - 10) log_{4х - 3}(x² - 4х + 9) ≥ 0.

Решение:

В правой части неравенства стоит 0, в левой — произведение двух множителей. Определим знаки каждого из этих множителей.

При x = 10/7 выражение 7x − 10 = 0, при x > 10/7 выражение 7x − 10 > 0, а при x < 10/7 выражение 7x − 10 < 0.

Рассмотрим выражение log_4x−3(x² − 4x + 9). Заметим, что x² − 4x + 9 = (x − 2)² + 5 ≥ 5 при любых значениях x. Значит, при 4x − 3 > 1, то есть при x > 1, выражение log_4x−3(x² − 4x + 9) > 0; при 0 < 4x − 3 < 1, то есть при 3/4 < x < 1, log_4x−3(x² − 4x + 9) < 0 и не определено при x ≤ 3/4 и x = 1.

Удобно знаки сомножителей отметить на двух параллельных прямых.

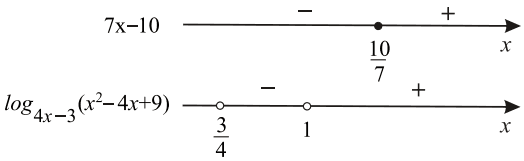
Таким образом, решение исходного неравенства: 3/4 < x < 1; x ≥ 10/7 .

Ответ: (3/4 ; 1) ; (10/7 ; +∞).