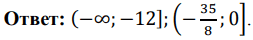Решите неравенство log_11(8x^2 + 7) - log_11(x^2 + x + 1) >= log_11...
Категория: Задание 15 ЕГЭ по математике (Неравенства)
Задание:
Решите неравенство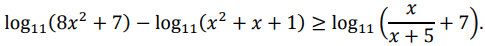 
Решение:
Правая часть неравенства определена при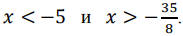 
. Поскольку при любых значениях x выражение 8x2 + 7 принимает положительные значения, при 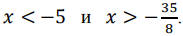неравенство принимает вид:
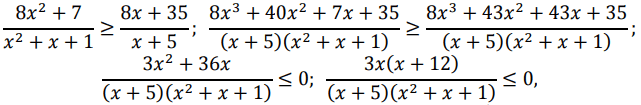
откуда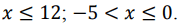 
. Учитывая ограничения 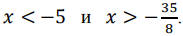, получаем: 
.
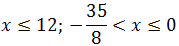