Скорость автомобиля, разгоняющегося с места старта...

Задание:

Скорость автомобиля, разгоняющегося с места старта по прямолинейному отрезку пути длиной l км с постоянным ускорением a км/ч² , вычисляется по формуле 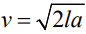 . Определите наименьшее ускорение, с которым должен двигаться автомобиль, чтобы, проехав один километр, приобрести скорость не менее 100 км/ч. Ответ выразите в км/ч² .

Решение:

Задача сводится к решению уравнения 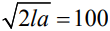 для длины пути l =1 км:

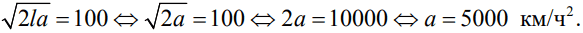
Если ускорение автомобиля будет превосходить найденное, то, проехав один километр, гонщик наберет большую скорость, поэтому наименьшее необходимое ускорение равно 5000 км/ч².

Заметим, что кажущееся на первый взгляд большим ускорение 5000 км/ч², выраженное привычных нам в метрах в секунду, на самом деле небольшое; автомобиль действительно может его приобрести.

Ответ: 5000