Стороны основания правильной треугольной пирамиды равны 16,...

Стороны основания правильной треугольной пирамиды равны 16, а боковые рёбра равны 17. Найдите площадь боковой поверхности этой пирамиды.

Решение:

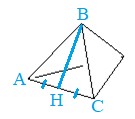
Поскольку треугольник ABC – равнобедренный, то высота BH является также и медианой, то есть AH = CH = 16 / 2 = 8.
Рассмотрим прямоугольный треугольник ABH: AB = 17, AH = 8.
По теореме Пифагора найдем BH:

BH² = AB² – AH² = 17² – 8² = 225.
BH = 15.

Найдем площадь боковой грани ABC:
S_гр = ½ * AC * BH = ½ * 16 * 15 = 120.
Площадь боковой поверхности состоит из трех площадей боковой грани: S_пов = S_гр * 3 = 120 * 3 = 360.

Ответ: 360.