В прямоугольной трапеции АВСD с основаниями ВС и АD угол ВAD прямой...

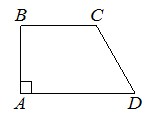
В прямоугольной трапеции АВСD с основаниями ВС и АD угол ВAD прямой, АВ=12, ВС=CD=13 (см. рисунок). Найдите среднюю линию трапеции.

Решение:

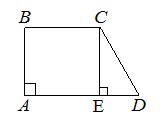
Проведем высоту к стороне трапеции AD. Получился прямоугольный треугольник CDE, у которого сторона CE = AB.

Найдем ED по теореме Пифагора:
ED² = CD² – CE² = 13² – 12² = 25.
ED = 5.
ABCE является квадратом, поскольку его стороны равны, а углы прямые. Значит AE = BC = 13.
Нижнее основание AD = AE + ED = 13 + 5 = 18.
Теперь, когда оба основания трапеции известны, найдем среднюю линию: средняя линия = (AD + DC) / 2 = (18 + 13) / 2 = 15,5.

Ответ: 15,5