В равнобедренном треугольнике ABC боковая сторона AB=25, sinA=3/5...

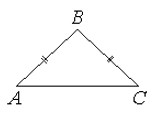
В равнобедренном треугольнике ABC боковая сторона AB=25, sinA=3/5. Найдите площадь треугольника ABC.

Решение:

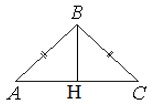
Проведем высоту BH в треугольнике ABC. Поскольку треугольник равнобедренный, то высота также является и медианой.
Синус угла A рассчитывается по формуле:

sinA = BH / AB.

Выразим из формулы сторону BH:

BH = sinA * AB = (3 / 5) * 25 = 15.

По теореме Пифагора найдем сторону AH треугольника ABH:
AH² = AB² – BH²
AH² = 25² – 15² = 400
AH = 20
Так как BH является медианой и делит сторону AC пополам, то сторона AC = 2 * AH = 2 * 20 = 40.

Теперь найдем площадь треугольника по имеющимся данным: S = 0.5 * AC * BH = 0.5 * 40 * 15 = 300.

Ответ: 300.