В равнобедренном треугольнике ABC основание AC равно 40,...

В равнобедренном треугольнике ABC основание AC равно 40, площадь треугольника равна 300. Найдите длину боковой стороны AB.

Решение:

Обратимся к формуле площади треугольника:

S = 0.5 * h * a,

где h – высота треугольника, a – основание треугольника.

Из формулы площади выразим высоту:

h = S / (0.5 * a) = 300 / (0.5 * 40) = 15.

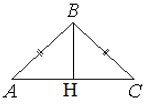
Поскольку треугольник равнобедренный, то высота опускается к основанию под прямым углом и делит треугольник на два равных прямоугольных треугольника (третье свойство равнобедренного треугольника).

Рассмотрим треугольник ABH: сторона BH = h = 15, сторона AH = AC / 2 = 40 / 2 = 20.
Тогда по теореме Пифагора найдем гипотенузу AB треугольника ABH:
AB² = BH² + AH²
AB² = 15² + 20² = 625
AB = 25

Ответ: 25