Найдите все положительные значения а, при...

Задание:

Найдите все положительные значения а, при каждом из которых система:

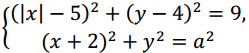
имеет единственное решение.

Решение:

Если x ≥ 0 ,  то уравнение  (|x| - 5)² + (y - 4)² = 9 задаёт окружность ω₁ с центром в точке C₁(5;4) радиусом 3, а если x < 0, то оно задаёт окружность ω₂ c центром в точке C₂(-5;4) таким же 
радиусом (см. рисунок).

При  положительных значениях  а  уравнение (x + 2)² + y² = a² задаёт  окружность с центром в точке C(-2;0) радиусом а. Поэтому задача состоит в том, чтобы найти все значения  а,  при  каждом  из  которых  окружность ω имеет единственную  общую  точку  с  объединением  окружностей  ω₁ и ω₂  .

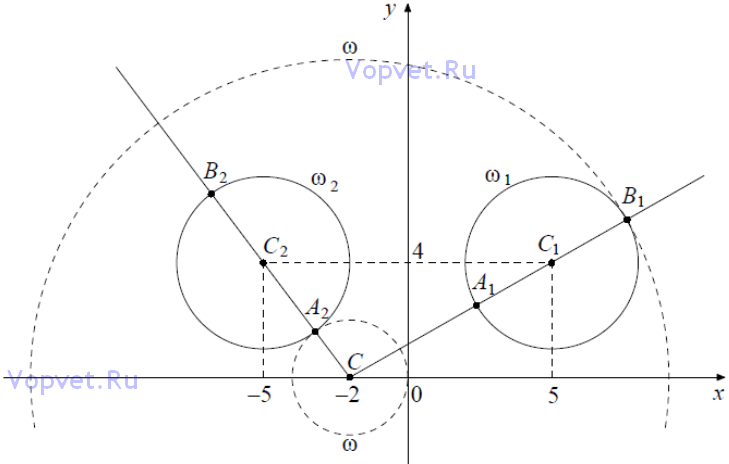
Исходная  система  имеет  единственное  решение  тогда  и  только  тогда,  когда  окружность ω  касается  ровно  одной  из  двух  окружностей  ω₁  и  ω₂  и  не  пересекается  с  другой.  Так  как CA₂ < CA₁ < CB₂ < CB₁, то условию задачи удовлетворяют только числа a = 2 и a = √65 + 3

Ответ: 2; √65 + 3