Найдите все значения а, при которых система урав...

Задание:

Найдите все значения а, при которых система уравнений 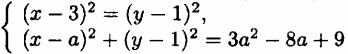 имеет ровно три решения.

Решение:

Уравнение (x − 3)² = (y − 1)² равносильно совокупности двух уравнений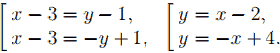  

Множество решений этой совокупности совпадает с множеством всех точек, лежащих на двух прямых: y = x − 2 и y = −x + 4. Заметим, что эти прямые проходят через точку (3; 1), так как система 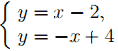 имеет единственное решение (3; 1).

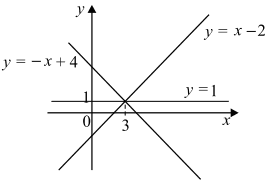
При каждом значении a множеством решений второго уравнения системы

(x − a)² + (y − 1)² = 3a² − 8a + 9 будет множество всех точек окружности с центром в точке (a; 1), лежащей на прямой y = 1, и радиусом 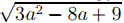 (заметим, что 3a² − 8a + 9 > 0 для любого a).

Указанные окружности будут иметь ровно три общие точки с парой указанных выше пересекающихся прямых в том и только том случае, когда окружность проходит через точку пересечения этих прямых.

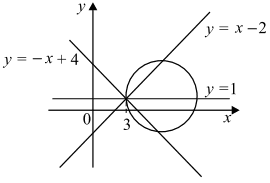
В таком случае точка (3; 1) лежит на окружности, значит, верно равенство

(3 − a)² + (1 − 1)² = 3a² − 8a + 9.

Отсюда получаем: 9 − 6a + a² = 3a² − 8a + 9; 2a² − 2a = 0;

2a * (a − 1) = 0; a = 0 или a = 1.

Ответ: 0; 1.