Найдите все значения параметра а, при которых ур...

Задание:

Найдите все значения параметра а, при которых уравнение 

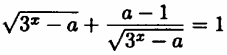
имеет ровно два различных корня.

Решение:

После приведения к общему знаменателю уравнение примет вид 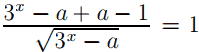 или 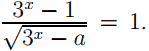 Пусть 3^x = t, t > 0. Заметим, что после замены каждому положи- тельному корню уравнения  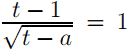соответствует единственный корень исходного уравнения (это следует из монотонности функции 3^x = t). Уравнение  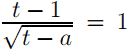равносильно системе

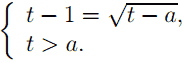
Возведём в квадрат обе части первого уравнения, учитывая, что t ≥ 1:

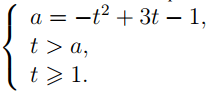
Решим систему графически в системе координат tOa.

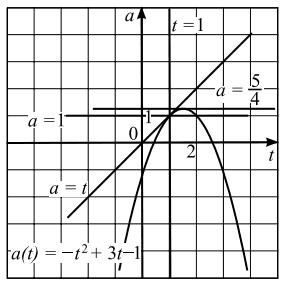
Вершина параболы a = −t² + 3t − 1 — точка с координатами (3/2 ; 5/4). Графики функций a = −t² + 3t − 1 и a = t имеют единственную общую точку t = 1. Множество точек, удовлетворяющих неравенству a < t, представляет собой полуплоскость, лежащую ниже прямой a = t.

−t² + 3t − 1 = t, t² − 2t + 1 = 0, t = 1.

По графику видно, что парабола a = −t² + 3t − 1 и прямая a = const имеют ровно две общие точки при условии t ≥ 1, если 1 ≤ a < 5/4 , значит, исходное уравнение имеет ровно два корня при этих же значениях a.

Ответ: [1; 5/4).