Периметр прямоугольной трапеции, описанной...
Категория: Задание 6 ЕГЭ по математике (Планиметрия)
Задание:
Периметр прямоугольной трапеции, описанной около окружности, равен 32, её большая боковая сторона равна 9. Найдите радиус окружности.
Решение:
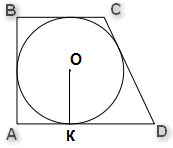
* В любом описанном четырехугольнике суммы противоположных сторон равны:
BC + AD = AB + CD
AB + BC + AD + CD = 32
* BC + AD = AB + CD = 32/2 = 16
* Большая сторона = 9, меньшую(AB) обозначим за X:
9 + x = 16
x = 16 - 9 = 7
* Радиус окружности(OK) равен половине AB = 1/2 * 7 = 3.5
Ответ: 3.5