Решение 91-го варианта с сайта А.Ларина..

Разберем 91 тренировочный вариант с сайта Александра Ларина. 

Вариант расположен здесь

Номер 1:

Ежемесячная плата за воду по тарифу составляет 70 рублей с одного
проживающего в квартире человека. Плата по счетчику составляет 15 рублей за 1 м³ воды. Семья из трех человек в среднем за месяц потребляет 6 м³ воды. Сколько рублей эта семья будет экономить ежегодно, если установит у себя в квартире водяной счетчик?

Решение: 

* По тарифу 70 рублей с одно человека, семья из трех человек = 70 * 3 = 210 руб.
* 15 * 6 = 90 рублей ежемесячная оплата по счетчику.
* Экономия в месяц = 210 - 90 = 120 рублей.
* Годовая экономия = 12 * 120 = 1440

Ответ: 1440

Номер 2:

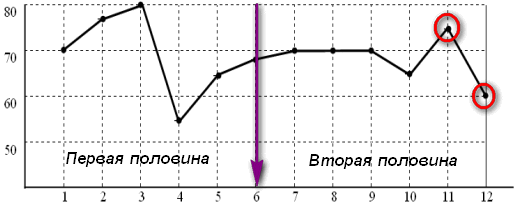
* Главное условие задачи - это насчет второй половины 2006 года. На рисунке отмечаем себе вторую половину и находим наибольшую и наименьшую цену.

* Наибольшая равна 75, так как она находится в центре между 70 и 80 долларами.
* Наименьшая равна 60 долларам.
* Разность = 75 - 60 = 15 долларов

Ответ: 15

Номер 3:

Независимая экспертная лаборатория определяет рейтинг R бытовых приборов на основе коэффициента ценности, равного 0,001 средней цены Р, показателей функциональности F, качества Q и дизайна D. Каждый из показателей оценивается целым числом от 0 до 4. Итоговый рейтинг вычисляется по формуле R=4(2F+ 2Q + D) –0,001Р. В таблице даны средняя цена и оценки каждого показателя для нескольких моделей электрических чайников. Определите наивысший рейтинг представленных в таблице
моделей электрических чайников

Решение:

Для A: R = 4(2 * 1 + 2 * 0 + 0) - 0.001 * 4000 = 4 * 2 - 4 = 4
Для Б: R = 4(2 * 4 + 2 * 3 + 0) - 0.001 * 4500 = 4 * 14 - 4.5 = 56 - 4.5 = 51.5
Для В: R = 4(2 * 2 + 2 * 3 + 0) - 0.001 * 4400 = 4 * 10 - 4.4 = 40 - 4.4 = 35.6
Для Г: R = 4(2 * 2 + 2 * 3 + 4) - 0.001 * 4200 = 4 * 14 - 4.2 = 56 - 4.2 = 51.8

Наивысший рейтинг равен 51.8

Ответ: 51.8

Номер 4:

Клетка имеет размер 1 см × 1 см. Найдите периметр фигуры, изображенной на рисунке. Ответ дайте в сантиметрах.

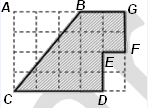
Решение:

* Периметр любой фигуры равен сумме длин всех его сторон:
  По теореме Пифагора найдем длину стороны BC:
  BC² = AB² + AC² = 3² + 4²
  BC² = 9 + 16 = 25
  BC = 5

* Периметр фигуры равен: BC + CD + DE + EF + FG + BG = 5 + 4 + 2 + 1 + 2 + 2 = 16

Ответ: 16

Номер 5:

Какова вероятность того, что при бросании двух игральных кубиков выпадут числа,сумма которых делится на 5? Ответ округлите до сотых

Решение:

* При бросании двух кубиков могут быть следующие варианты:

1 - 1   2 - 1    3 - 1    4 - 1    5 - 1    6 - 1
1 - 2   2 - 2    3 - 2    4 - 2    5 - 2    6 - 2
1 - 3   2 - 3    3 - 3    4 - 3    5 - 3    6 - 3
1 - 4   2 - 4    3 - 4    4 - 4    5 - 4    6 - 4
1 - 5   2 - 5    3 - 5    4 - 5    5 - 5    6 - 5
1 - 6   2 - 6    3 - 6    4 - 6    5 - 6    6 - 6

* Всего 36 исходов (6 цифр по 6 исходов)

* Теперь посчитаем количество исходов, где сумма кратна 5: их 7
* Вероятность равна: 7/36 = 0.1944.., нас просят округлить до сотых:
  Вероятность равна 0.19

Ответ: 0.19

Номер: 6

Найдите корень уравнения (2x + 7)³ = 125.

Решение:    

(2x + 7)³ = 5³        Проверка:
2x + 7 = 5               x = -1
2x = 5 - 7                (2 * (-1) + 7)³ = 125
2x = -2                    (-2 + 7)³ = 125
x = -1                       5³ = 125

Ответ: -1

Номер 7:

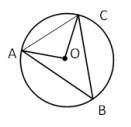
Точка О – центр окружности (рис.). ∠САО = 50º. Найдите ∠АВС. Ответ дайте в градусах

Решение:

Рассмотрим треугольник AOC:
* AO = OC - радиусы окружности => треугольник равнобедренный.
* ∠A = ∠C = 50º - углы при основании равнобедренного треугольника.
* ∠O = 180º - 50º - 50v = 80º.

* Рассмотрим треугольник ABC:
  ∠B = 1/2 ∠O - вписанный угол в два раза меньше центрального.
  ∠B = 80º : 2 = 40º

Ответ: 40

Номер 8:

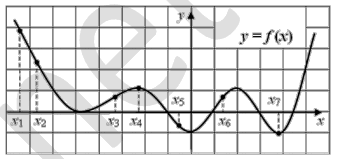
На графике дифференцируемой функции у = f(x) отмечены семь точек: х1, х2, …, х7. В скольких из этих точек производная функции у = f'(x) отрицательна?

Решение:

* Производная отрицательна там, где функция убывает.
* Таких точек у нас 3 -  (x1, x2, x5)

Ответ: 3

Номер 9:

Найдите боковое ребро правильной четырехугольной призмы (рис.), если сторона ее основания равна 2, а площадь боковой поверхности равна 24. 

Решение:

* Площадь боковой поверхности призмы равна сумма площадей ее боковых граней.
* Так как призма правильная, значит в основании квадрат, следовательно все стороны равны 2.
* Обозначим боковое ребро за x - ее нам нужно найти:
* Боковые грани - прямоугольники. Площадь прямоугольника равна произведению длины на ширину = 2 * x
* Так как призма четырехугольная, значит у нее 4 боковых граней:
  Площадь боковой поверхности = 4 * 2 * x
  24 = 4 * 2 * x
  24 = 8 * x
  x = 24/8
  x = 3

Ответ: 3

Номер 10:

Найдите значение выражения: √12 * cos² 5п/12 - √3.

Ответ: -1.5

Решение:

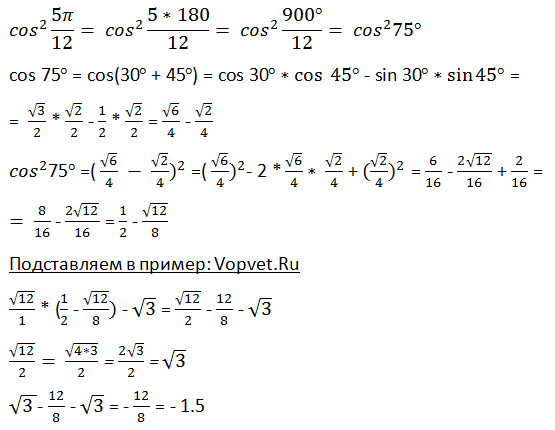
Номер 11:

Деталью некоторого прибора является вращающаяся катушка. Она состоит из трeх однородных соосных цилиндров: центрального массой m=8 кг и радиуса R=10 см, и двух боковых с массами M=1 кг и с радиусами R+h. При этом момент инерции катушки
относительно оси вращения, выражаемый в кг*см^2 задаeтся формулой:

I = ((m + 2M)R^2)/2 + M(2Rh + h^2). При каком максимальном значении h момент инерции катушки не превышает предельного значения 625 кг*см2 ? Ответ выразите в сантиметрах.

 

Ответ: 5

Решение: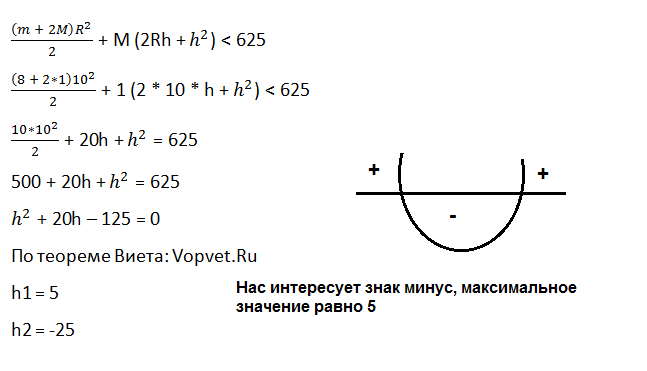Номер 12:

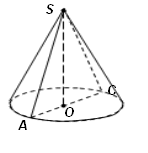
Образующая конуса равна 20, а диаметр основания равен 24. Найдите высоту конуса.

Решение:

* AC - диаметр основания, по условию равен 12.
* AO = OC - радиусы основания = 1/2 * AC = 12
* SO - Высота, ее нужно найти.
* Рассмотри треугольник SOC (∠O = 90º)
  SC² = SO² + OC²
  20² = SO² + 12²
  400 = SO² + 144
  SO² = 400 - 144
  SO² = 256
  SO = 16

Ответ: 16

Номер 13:

Из одной точки круговой трассы, длина которой равна 14 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.

Решение:

* Обозначим скорость второго автомобиля за x км/ч. 
* Известно, что через 2/3 часа первый автомобиль опережал второго на 14 км (на один  круг)
* Решаем относительно расстояния:
  S₁ = 80 * 2/3
  S₂ = x * 2/3
* S₁ = S₂ + 14
  80 * 2/3 = x * 2/3 + 14
  160/3 = 2x/3 + 14
  160/3 - 14 = 2x/3
  118/3 = 2x/3
   6x = 354
   x = 59

Ответ: 59

Номер 14:

Найдите абсциссу точки графика функции g(x) = x³ + (√5 −12x)², касательная
в которой параллельна прямой у = 15x – 2 или совпадает с ней.

Решение:

ОДЗ:

5 - 12x >= 0
-12x >= -5
 x <= 5/12

---

g(x) = x³ + 5 - 12x
g'(x) = 3x² - 12
y' = 15

g'(x) = y'

3x² - 12 = 15
3x² = 27
x² = 9
x = 3 - посторонний корень по ОДЗ.
x = -3

Ответ: -3